4. 两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”).

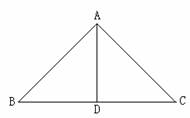例1.在△ABC中，AB=AC，AD是三角形的中线.

求证：△ABD≌△ACD

例2.如图所示，直线AD、BE相交于点C，AC=DC，BC=EC.

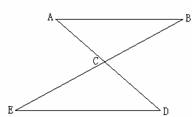求证：AB=DE

例3.如图所示，D在AB上，E在AC上，AB=AC, ∠B=∠C.

求证：AD=AE

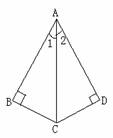例4.如图，AB⊥BC, AD⊥DC, ∠1=∠2.

求证：AB=AD

练习：

3. 两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).

2. 两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”).

1. 三边对应相等的两个三角形全等(可以简写成“边边边”或“SSS”).

全等形：能够完全重合的图形叫做全等形.

全等三角形：能够完全重合的两个三角形叫做全等三角形.

对应顶点、对应边、对应角：把两个全等的三角形重合到一起.重合的顶点叫做对应顶点；重合的边叫做对应边；重合的角叫做对应角.

7．在等腰△ABC中，AB=AC．

　(1)若M是BC的中点，过M任作一直线交AB，AC(或其延长线)于D，E，求证：2AB＜AD+AE．

　(2)若P是△ABC内一点，且PB＜PC，求证：∠APB＞∠APC．

本资料由《七彩教育网》 提供！

6．在△ABC中，AB＞AC，AD为高，P为AD上的任意一点，求证：

PB-PC＞AB-AC．

5．在△ABC中，BE和CF是高，AB＞AC，求证：

AB+CF≥AC+BE．

4．设△ABC中，∠C＞∠B，BD，CE分别为∠B与∠C的平分线，求证：BD＞CE．

3．已知△ABC的边BC上有两点D，E，且BD=CE，求证：AB+AC＞AD+AE．