8．已知13x²-6xy+y²-4x+1=0，求(x+y)13·x10的值．

本资料由《七彩教育网》 提供！

5．设a+b+c=3m，求(m-a)³+(m-b)³+(m-c)³-3(m-a)(m-b)(m-c)的值．

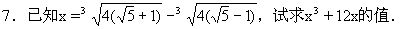
3．已知a-b+c=3，a²+b²+c²=29，a³+b³+c³=45，求ab(a+b)+bc(b+c)+ca(c+a)的值．

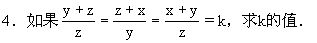
2．已知x+y=a，x²+y²=b²，求x⁴+y⁴的值．

5．利用分式、根式的性质求值

　分式与根式的化简求值问题，内容相当丰富，因此设有专门讲座介绍，这里只分别举一个例子略做说明．

　例10 已知xyzt=1，求下面代数式的值：

　分析 直接通分是笨拙的解法，可以利用条件将某些项的形式变一变．

　解 根据分式的基本性质，分子、分母可以同时乘以一个不为零的式子，分式的值不变．利用已知条件，可将前三个分式的分母变为与第四个相同．

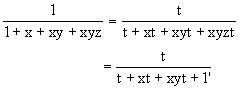
　同理

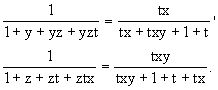
　分析 计算时应注意观察式子的特点，若先分母有理化，计算反而复杂．因为这样一来，原式的对称性就被破坏了．这里所言的对称性是分利用这种对称性，或称之为整齐性，来简化我们的计算．

　同样(但请注意算术根！)

　将①，②代入原式有

练习六

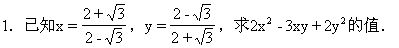
4．利用非负数的性质求值

　若几个非负数的和为零，则每个非负数都为零，这个性质在代数式求值中经常被使用．

　例8 若x²-4x+|3x-y|=-4，求y^x的值．

　分析与解 x，y的值均未知，而题目却只给了一个方程，似乎无法求值，但仔细挖掘题中的隐含条件可知，可以利用非负数的性质求解．

　因为x²-4x+|3x-y|=-4，所以

　x²-4x+4+|3x-y|=0，

　即 (x-2)²+|3x-y|=0．

　所以 y^x=6²=36．

　例9 未知数x，y满足

　(x²+y²)m²-2y(x+n)m+y²+n²=0， 其中m，n表示非零已知数，求x，y的值．

　分析与解 两个未知数，一个方程，对方程左边的代数式进行恒等变形，经过配方之后，看是否能化成非负数和为零的形式．

　将已知等式变形为

　m²x²+m²y²-2mxy-2mny+y²+n²=0，

　(m²x²-2mxy+y²)+(m²y²-2mny+n²)=0，即 (mx-y)²+(my-n)²=0．

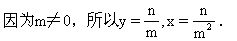
3．设参数法与换元法求值

　如果代数式字母较多，式子较繁，为了使求值简便，有时可增设一些参数(也叫辅助未知数)，以便沟通数量关系，这叫作设参数法．有时也可把代数式中某一部分式子，用另外的一个字母来替换，这叫换元法．

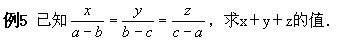
　分析 本题的已知条件是以连比形式出现，可引入参数k，用它表示连比的比值，以便把它们分割成几个等式．

　x＝(a-b)k，y＝(b-c)k，z＝(c-a)k．

　所以

　x+y+z=(a-b)k+(b-c)k+(c-a)k=0．

　u+v+w=1，①

　由②有

　把①两边平方得

　u²+v²+w²+2(uv+vw+wu)=1，

　所以u²+v²+w²=1，

　即

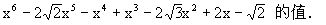
　两边平方有

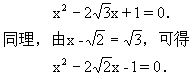
　所以

2．利用乘法公式求值

　例3 已知x+y=m，x³+y³=n，m≠0，求x²+y²的值．

　解 因为x+y=m，所以

　m³=(x+y)³=x³+y³+3xy(x+y)=n+3m·xy，

　所以

　求x²+6xy+y²的值．

　分析 将x，y的值直接代入计算较繁，观察发现，已知中x，y的值正好是一对共轭无理数，所以很容易计算出x+y与xy的值，由此得到以下解法．

　解 x²+6xy+y²=x²+2xy+y²+4xy

　　　　 =(x+y)²+4xy

1．利用因式分解方法求值

　因式分解是重要的一种代数恒等变形，在代数式化简求值中，经常被采用．

　分析 x的值是通过一个一元二次方程给出的，若解出x后，再求值，将会很麻烦．我们可以先将所求的代数式变形，看一看能否利用已知条件．

　解 已知条件可变形为3x²+3x-1=0，所以

　6x⁴+15x³+10x²

　=(6x⁴+6x³-2x²)+(9x³+9x²-3x)+(3x²+3x-1)+1

　=(3x²+3x-1)(2z²+3x+1)+1

　=0+1=1．

　说明 在求代数式的值时，若已知的是一个或几个代数式的值，这时要尽可能避免解方程(或方程组)，而要将所要求值的代数式适当变形，再将已知的代数式的值整体代入，会使问题得到简捷的解答．

　例2 已知a，b，c为实数，且满足下式：

　a²+b²+c²=1，①

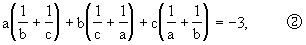
　求a+b+c的值．

　解 将②式因式分解变形如下

　即

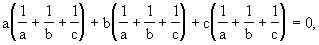
　所以

　a+b+c=0或bc+ac+ab=0．

　若bc+ac+ab=0，则

　(a+b+c)²=a²+b²+c²+2(bc+ac+ab)

　　　=a²+b²+c²=1，

　所以 a+b+c=±1．所以a+b+c的值为0，1，-1．

　说明 本题也可以用如下方法对②式变形：

　即

　前一解法是加一项，再减去一项；这个解法是将3拆成1+1+1，最终都是将②式变形为两个式子之积等于零的形式．

12. 填空题：

(1)如图1，已知:AC =DB，要使≌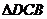，只需增加一个条件是_____　 ____.

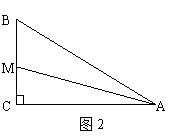
(2)如图2,已知:中，，AM平分，CM =20cm那么M到AB的距离

是　　　　　　 .

(3)如图3,已知:在和中，如果AB =DE，BC =EF，只要找出　　 =　　 或　　　 =　　　　

或　　　 //　　　 ，就可证得≌.

(4). 已知:如图4，AB =EB，∠1=∠2，∠ADE =120°，AE、BD相交于F，则∠3的度数为___　　　 ___．

(5). 如图5, 已知：∠1 =∠2 , ∠3 =∠4 , 要证BD =CD , 需先证△AEB ≌△A EC , 根据是_________再证△BDE ≌△__　 ____ , 根据是__　 ________．

(6). 已知：如图6 , AC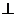BC于C , DE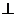AC于E , AD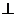AB于A , BC =AE．若AB = 5 , 则AD =___________．