2.5:X=1:5000　 解得X=12500厘米=125米

所以, A、B两建筑物之间的实际距离为125米.　 ………………………2分

24. 证明:　 ∵DE∥AB　　　　　　　 (画出图形2分)

∴ ∠A=∠E　　　　 ……………………1分

在△ABC和△EDC中

　　 ∠A=∠E

∵　 ∠ACB=∠DCE　　

BC=CD

　　　　 ∴　 △ABC≌△EDC　　 (AAS) ……………………2分

∴　 AB=DE　　　　 ………………………3分

量得　 AB=2.5㎝　　 ……………………1分

23.(1)距离与时间之间的关系;　　 超市离家900米……………………2分

　 (2)小明在超市待了10分钟,　 小明从超市回到家花了15分钟 ……………2分

(3)小明从家到超市的平均速度是900÷20=45米/分钟,……………………1分

(4)设函数关系式为y=kx+b　 则

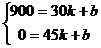解得　 ………………1分

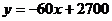∴　 　　　…………………………2分

22.证明:　 ∵ M是AB的中点

∴　 AM=BM　　　 ……………………2分

在△ACM和△BDM中

　　 AM=BM

∵　 ∠1=∠2

MC=MD

　　　　 ∴　 △ACM≌△BDM　　 (SAS) ……………………5分

∴　 AC=BD　　　　 ………………………6分

21.(1)39.1℃…………………………………2分

(2)14-18时…………………………………2分

(3)您的体温正在下降,请别担心.等,只要符号图形都得分. …………………2分

(11),　 x, y;　　　　 (12). x≥3　　　 (13). m=4　　　　　 (14).　 25,　 1;　

(15).二，四；减小　　 　　　(16).　 k=3.　 　　(17). 70⁰,　 15㎝　

(18). ∠ABC　 或∠CBA　　　 (19). BC=DE,或∠A =∠F或AB∥EF　 　

　 (20).　 y=4x　 (x>40)不写自变量范围不扣分

ACCAD　　 CCBDB

27．(9分) 甲骑自行车、乙骑摩托车沿相同路线由A地到B地，行驶过程中路程与时间的函数关系的图象如图. 根据图象解决下列问题：

(1)　　　　 先出发，先出发　　　　 分钟。

　　　 　　　　　先到达终点，先到　　　　 分钟。

(3) 在什么时间段内，两人均行驶在途中(不包括起点和终点)，在这一时间段内，请你根据下列情形填空：

当　　　　　　　　 时，甲在乙的前面时；

当　　　　　　　　 时，甲与乙相遇时；

当　　　　　　　　 时，甲在乙后面.

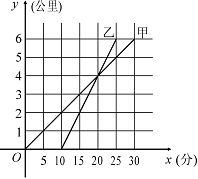(2) 分别求出甲、乙两人的行驶速度；

28，(10分)一次函数y=kx-2的图象经过点A(2，4).

(1)求这个函数的解析式；

(2)请判断点B(-2，-6)是否在这个函数的图象上，并说明理由.

(3)若这个函数与x轴交于C点，与y轴交于D点，求△OCD的面积。

26.(8分)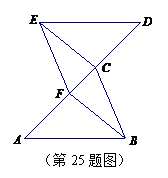已知:如图,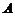、、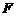、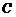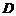四点在一直线上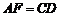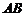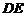，，∥，且．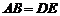

求证：(1)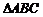≌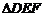；(2)BC∥EF.

24.(7分)如图，A、B两建筑物位于河的两岸，要测得它们之间的距离，可以从B点出发沿河岸画一条射线BF，在BF上截取BC=CD，过D作DE∥AB，使E、C、A在同一直线上，则DE的长就是A、B之间的距离，请你作出草图并说明道理.若图是按1︰5000的比例画出, 那么A、B两建筑物之间的距离是多少米？

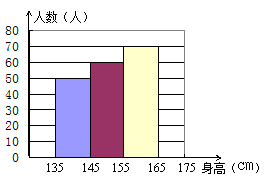25，为了了解我县八年级女生的身高情况，在我校八年级女生中随机抽测了200名女生的身高，统计数据如下：(6分)

请你结合所给数据，回答下列问题：

(1)表中的P=　　 　　， Q=　　　 。

(2)请把直方图补充完整。

(3)估计我县八年级女生的身高大约为　　　　 ㎝