5．证明：

3．求证：

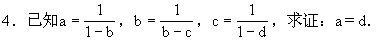
2．证明：

　(x+y+z)³xyz-(yz+zx+xy)³

　=xyz(x³+y³+z³)-(y³z³+z³x³+x³y³)．

1．已知(c-a)²-4(a-b)(b-c)=0，求证：2b=a+c．

4．其他证明方法与技巧

　求证：8a+9b+5c=0．

　a+b=k(a-b)，b+c=2k(b-c)，

　(c+a)=3k(c-a)．

　所以

　6(a+b)=6k(a-b)，

　3(b+c)=6k(b-c)，

　2(c+a)=6k(c-a)．以上三式相加，得

　6(a+b)+3(b+c)+2(c+a)

　=6k(a-b+b-c+c-a)，

　即 8a+9b+5c=0．

　说明 本题证明中用到了“遇连比设为k”的设参数法，前面的例2用的也是类似方法．这种设参数法也是恒等式证明中的常用技巧．

　例8 已知a+b+c=0，求证

　2(a⁴+b⁴+c⁴)＝(a²+b²+c²)²．

　分析与证明 用比差法，注意利用a+b+c=0的条件．

　左-右=2(a⁴+b⁴+c⁴)-(a²+b²+c²)²

　　=a⁴+b⁴+c⁴-2a²b²-2b²c²-2c²a²

　　=(a²-b²-c²)²-4b²c²

　　=(a²-b²-c²+2bc)(a²-b²-c²-2bc)

　　=[a²-(b-c)²][a²-(b+c)²]

　　=(a-b+c)(a+b-c)(a-b-c)(a+b+c)=0．所以等式成立．

　说明 本题证明过程中主要是进行因式分解．

　分析 本题的两个已知条件中，包含字母a，x，y和z，而在求证的结论中，却只包含a，x和z，因此可以从消去y着手，得到如下证法．

　证 由已知

　说明 本题利用的是“消元”法，它是证明条件等式的常用方法．

　例10 证明：

　(y+z-2x)³+(z+x-2y)³+(x+y-2z)³

　=3(y+z-2x)(z+x-2y)(x+y-2z)．

　分析与证明 此题看起来很复杂，但仔细观察，可以使用换元法．令

y+z-2x=a，①

z+x-2y=b，②

x+y-2z=c，③

　则要证的等式变为

a³+b³+c³=3abc．

　联想到乘法公式：

　a³+b³+c³-3abc=(a+b+c)(a²+b²+c²-ab-bc-ca)，所以将①，②，③相加有

　a+b+c=y+z-2x+z+x-2y+x+y-2z=0，

　所以 a³+b³+c³-3abc=0，

　所以

　(y+z-2x)³+(z+x-2y)³+(x+y-2z)³

　=3(y+z-2x)(z+x-2y)(x+y-2z)．

　说明 由本例可以看出，换元法也可以在恒等式证明中发挥效力．

　例11 设x，y，z为互不相等的非零实数，且

　求证：x²y²z²=1．

　分析 本题x，y，z具有轮换对称的特点，我们不妨先看二元的

　所以x²y²=1．三元与二元的结构类似．

　证 由已知有

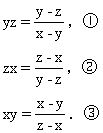
　①×②×③得x²y²z²=1．

　说明 这种欲进先退的解题策略经常用于探索解决问题的思路中．

　总之，从上面的例题中可以看出，恒等式证明的关键是代数式的变形技能．同学们要在明确变形目的的基础上，深刻体会例题中的常用变形技能与方法，这对以后的数学学习非常重要．

练习五

3．分析法与综合法

　根据推理过程的方向不同，恒等式的证明方法又可分为分析法与综合法．分析法是从要求证的结论出发，寻求在什么情况下结论是正确的，这样一步一步逆向推导，寻求结论成立的条件，一旦条件成立就可断言结论正确，即所谓“执果索因”．而综合法正好相反，它是“由因导果”，即从已知条件出发顺向推理，得到所求结论．

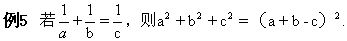
　证 要证 a²+b²+c²=(a+b-c)²，只要证

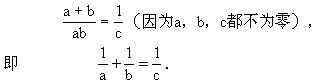
a²+b²+c²=a²+b²+c²+2ab-2ac-2bc，

　只要证 ab=ac+bc，

　只要证 c(a+b)=ab，

　只要证

　这最后的等式正好是题设，而以上推理每一步都可逆，故所求证的等式成立．

　说明 本题采用的方法是典型的分析法．

　例6 已知a⁴+b⁴+c⁴+d⁴=4abcd，且a，b，c，d都是正数，求证：a=b=c=d．

　证 由已知可得

a⁴+b⁴+c⁴+d⁴-4abcd=0，

　(a²-b²)²+(c²-d²)²+2a²b²+2c²d²-4abcd=0，

　所以

　(a²-b²)²+(c²-d²)²+2(ab-cd)²=0．

　因为(a²-b²)²≥0，(c2-d2)2≥0，(ab-cd)2≥0，所以

　a²-b²=c²-d²=ab-cd=0，

　所以 (a+b)(a-b)=(c+d)(c-d)＝0．

　又因为a，b，c，d都为正数，所以a+b≠0，c+d≠0，所以

　a＝b，c=d．

　所以

　ab-cd=a²-c²=(a+c)(a-c)=0，

　所以a＝c．故a=b＝c=d成立．

　说明 本题采用的方法是综合法．

2．比较法

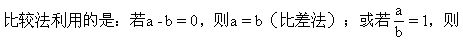　 a=b(比商法)．这也是证明恒等式的重要思路之一．

　例3 求证：

　分析 用比差法证明左-右=0．本例中，

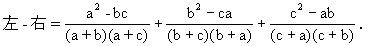
　这个式子具有如下特征：如果取出它的第一项，把其中的字母轮换，即以b代a，c代b，a代c，则可得出第二项；若对第二项的字母实行上述轮换，则可得出第三项；对第三项的字母实行上述轮换，可得出第一项．具有这种特性的式子叫作轮换式．利用这种特性，可使轮换式的运算简化．

　证 因为

　所以

　所以

　说明 本例若采用通分化简的方法将很繁．像这种把一个分式分解成几个部分分式和的形式，是分式恒等变形中的常用技巧．

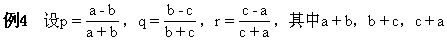　全不为零．证明：

　(1+p)(1+q)(1+r)=(1-p)(1-q)(1-r)．

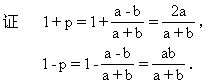
　同理

　所以

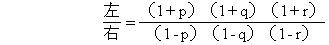
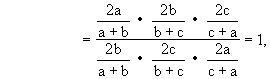
　所以(1+p)(1+q)(1+r)=(1-p)(1-q)(1-r)．

　说明 本例采用的是比商法．

1．由繁到简和相向趋进

　恒等式证明最基本的思路是“由繁到简”(即由等式较繁的一边向另一边推导)和“相向趋进”(即将等式两边同时转化为同一形式)．

　例1 已知x+y+z=xyz，证明：x(1-y²)(1-z²)+y(1-x²)(1-z²)+z(1-x²)(1-y²)=4xyz．

　分析 将左边展开，利用条件x+y+z=xyz，将等式左边化简成右边．

　证 因为x+y+z=xyz，所以

　左边=x(1-z²-y²-y²z²)+y(1-z²-x²+x²z²)+(1-y²-x²+x²y²)

　　=(x+y+z)-xz²-xy²+xy²z²-yz²+yx²+yx²z²-zy²-zx²+zx²y²

　　=xyz-xy(y+x)-xz(x+z)-yz(y+z)+xyz(xy+yz+zx)

　　=xyz-xy(xyz-z)-xz(xyz-y)-yz(xyz-x)+xyz(xy+yz+zx)

　　=xyz+xyz+xyz+xyz

　　=4xyz=右边．

　说明 本例的证明思路就是“由繁到简”．

　例2 已知1989x²=1991y²=1993z²，x＞0，y＞0，z＞0，且

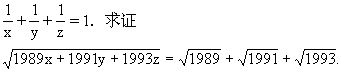
　证 令1989x²=1991y²=1993z²=k(k＞0)，则

　又因为

　所以

　所以

　说明 本例的证明思路是“相向趋进”，在证明方法上，通过设参数k，使左右两边同时变形为同一形式，从而使等式成立．

18、某工厂有220名员工，财务科要了解员工收入情况。现在抽测了10名员工的本月收入，结果如下：(单位：元)。

1660　 1540　 1510　 1670　 1620　 1580　 1580　 1600　 1620　 1620

(1)全厂员工的月平均收入是多少？

(2)平均每名员工的年薪是多少？

(3)财务科本月应准备多少钱发工资？

(4)一名本月收入为1570元的员工收入水平如何？

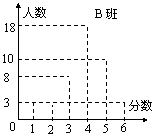
17、现有A、B两个班级，每个班级各有45名学生参加一次测试，每名参加者可获得0，1，2，3，4，5，6，7，8，9分这几种不同的分值中的一种．测试结果A班的成绩如下表所示，B班的成绩如右图所示．

(1)由观察可知，______班的方差较大；

(2)若两班合计共有60人及格，问参加者最少获______分才可以及格．