
题目列表(包括答案和解析)
2.联想与解题
例5 a,b为两个不相等且都不为零的数,同时有
a2+pa+q=0,b2+pb+q=0,
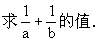
分析与解 由已知条件,联想到方程根的定义,a,b是方程x2+px+q=0的两个根,由a,b不为零,有
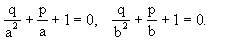

例6 如果(z-x)2-4(x-y)(y-z)=0,求证:
x+z=2y.
分析与解 (1)展开原式有
z2-2xz+x2-4(xy-y2-xz+yz)=0,
合并、配方得
(x+z)2-4y(x+z)+4y2=0,
即 (x+z-2y)2=0,
所以 x+z=2y.
(2)如果看已知条件:
(z-x)2-4(x-y)(y-z)=0,
很像二次方程根的判别式b2-4ac的形式,因此,可联想到方程
(x-y)t2+(z-x)t+(y-z)=0(x-y≠0)有二相等实根.由
(x-y)+(z-x)+(y-z)=0
可知1是以上方程的根,再由根与系数关系知

所以 x+z=2y.
当x=y=0,即x=y时,有x=y=z,所以
x+z=2y.
例7 化简

分析与解 这是一个根式的化简问题,分子、分母大同小异,自然联想到应用因式分解,使分子、分母具有公因式,化简就很容易了.
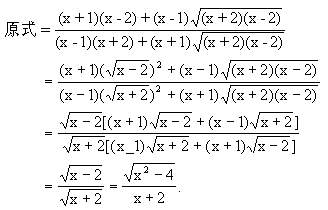
例8 图2-116是我国古代数学家赵爽证明勾股定理的“弦图”,其中“弦实”是弦平方的面积,“弦图”以弦为边作正方形(如正方形ABCD),然后在“弦图”内部作四个直角三角形(如△AHB,△BEC,△CDF,△DAG).设a,b,c为四个直角三角形的勾、股、弦,则根据“出入相补原理”就有

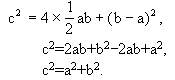
即 c2=2ab+b2-2ab+a2,
即 c2=a2+b2.
这是中国古代数学家独立于西方毕达哥拉斯和欧几里得发明的证法.后人沿用“出入相补原理”,也就是割补原理解决了许多数学问题,也创造了“勾股定理”的许多新证法.事实上每位初中同学,学了勾股定理,只要用心思考,一定会用割补法想出更新的证明勾股定理的方法.下面的几例,便是同学们提出的割补图.
设a,b,c分别为直角三角形的勾、股、弦.
(1)在图 2-117中,有

a2+b2=(S3+S5)+(S1+S2+S4)
=(S4+S5)+(S1+S2+S3)
=2S2+S1+S3=c2.
(2)在图 2-118中,有
a2+b2=(S3+S4)+(S1+S2)
=S1+S3+S4+S'2+S5=c2

(3)在图2-119中,有
a2+b2=(S2+S5)+(S1+S3+S4)
=S1+S2+S3+S4+S5=c2.
(4)在图2-120中,有
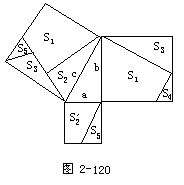
a2+b2=(S'2+S5)+(S1+S3+S4)
=(S'2+S4)+(S1+S3+S5)
=S1+S2+S3+S5=c2.
练习二十
1.类比与发现
例1 已知:△ABC中,∠C= 90°,AC=BC=1,BD是AC边上的中线,E点在AB边上,且ED⊥BD.求△DEA的面积(图2-113).
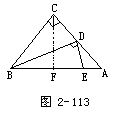
解 引CF⊥BA于F,由于BC= AC,所以CF是底边AB上的中线.因为H为△ABC的重心,所以

因为∠C=∠BDE=90°,所以
∠ADE=∠CBH.
又由∠A=∠BCH=45°,可知△ADE∽△CBH.所以
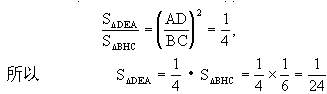
类比 如果保留例1中等腰三角形诸条件,去掉直角这一特殊性,那么是否会产生类似的命题呢?由此想到例2.

例2 如图2-114.已知△ABC中,∠C=4∠B=4∠A,BD是AC边上的中线,E点在AB上,且∠AED=∠C,S△ABC=1,求S△AED.
解 类似例1的解法,引CF⊥AB于F,交BD于H,显然△ADE不相似于△CBH.但由已知条件
∠C=4∠B=4∠A,
则
∠A=∠B=30°,∠C=120°.
由于CF平分∠C,所以
∠ACF=60°.
又因为∠AED=∠ACB,∠A=∠A,所以
△ADE∽△ABC,
所以

由于△AFC中∠AFC=90°,∠A=30°,所以若设CF=x,则
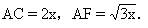

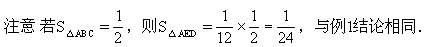
类比 如果保留例1中的直角等条件,去掉等腰三角形这一特殊性,可以类似地得到例3.
例3 已知△ABC中∠C= 90°,AC=2BC=2,BD是AC边上的中线,CF⊥AB于F,交BD于H(图2-115).求S△CBH.

解 本题直接求S△CBH有些困难,联想例1、例2中的△ADE,不妨引辅助线DE⊥BD交AB于E.
由于AC=2BC=2,D是AC的中点,且∠C=∠BDE=90°,所以
∠CBH=∠ADE=45°.
因为CF⊥AB于F,所以∠BCH=∠A.由于BC=AD=1,所以
△CBH≌△ADE,
所以 S△CBH=S△ADE.
因此只要求出S△ADE即可,为此,设DE=x,则
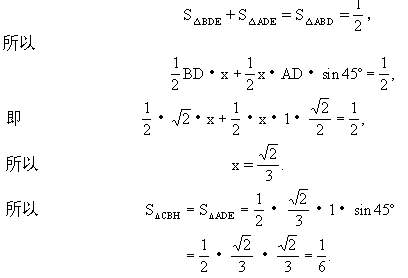
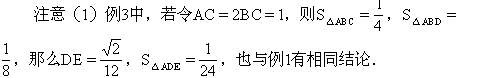
(2)例3由例1类比而来,最自然的想法是求S△ADE,为增加难度与变换方式获得新命题,故例3反求S△CBH.
我们知道一个三角形的三边如果是a,b,c,那么就有
│b-c│<a<b+c,①
即三角形任意一边小于其余两边之和,大于其余两边之差.
我们对①类比:是否有

存在呢?如果②存在,那么就发现了如下命题(例4).
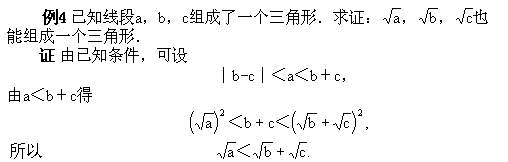

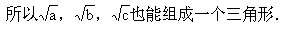
21、若2(x+1)-5<3(x-1)+4的最小整数解是方程 x-mx=5的解,求代数式
x-mx=5的解,求代数式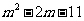 的值.
的值.
20、若关于 的方程组
的方程组 的解满足
的解满足 >
> ,求p的取值范围.
,求p的取值范围.
19、求不等式 ≤
≤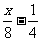 的非负数解.
的非负数解.
18、解下列不等式,并把解集在数轴上表示出来:
(1) (2)
(2) ≤1
≤1
(3)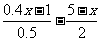 ≤
≤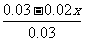 (4)
(4)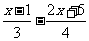 >-2
>-2
17、下面解不等式的过程是否正确,如不正确,请找出,并改正.
解不等式: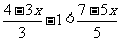
解:去分母,得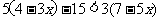 ①
①
去括号,得 ②
②
移项,合并,得 5<21 ③
因为x不存在,所以原不等式无解. ④
16、当k
时,代数式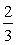 (k-1)的值不小于代数式1-
(k-1)的值不小于代数式1-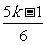 的值.
的值.
15、不等式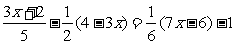 的非正整数解 _____.
的非正整数解 _____.
14、若关于x的不等式x-1≤a有四个非负整数解,则整数a的值为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com