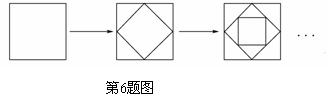
6. 如图，依次连结一个边长为1的正方形各边的中点，得到第二个正方形，再依次连结第二个正方形各边的中点，得到第三个正方形，按此方法继续下去， 则第六个正方形的面积是　　　 ．

5. 正方形的一条边长是3，那么它的对角线长是_______.

4. 下列命题中的假命题是(　 　)．

　　 A．一组邻边相等的平行四边形是菱形

　　 B．一组邻边相等的矩形是正方形

　　 c　 一组对边平行且相等的四边形是平行四边形

D．一组对边相等且有一个角是直角的四边形是矩形

3. 已知四边形ABCD是菱形，当满足条件_________时，它成为正方形(填上你认为正确的一个条件即可).

2. 在正方形ABCD中，AB=12 cm，对角线AC、BD相交于O，则△ABO的周长是(　　 )

A.12+12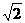　　　　 B.12+6　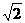　　 C.12+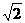　　　　　　　 D.24+6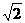

1. 四边形ABCD中，AC、BD相交于点O，能判别这个四边形是正方形的条件是(　　 )

A.OA=OB=OC=OD，AC⊥BD　　　　　 B.AB∥CD，AC=BD

C.AD∥BC，∠A=∠C　　　　　　　　 D.OA=OC，OB=OD，AB=BC

10.. 解：(1)∵四边形ABCD是平行四边形，∴∠1＝∠C，AD＝CB，AB＝CD ．

∵点E 、F分别是AB、CD的中点，∴AE＝AB ，CF＝CD ．

∴AE＝CF ．∴△ADE≌△CBF ．

(2)当四边形BEDF是菱形时，四边形 AGBD是矩形．

∵四边形ABCD是平行四边形，∴AD∥BC ．

∵AG∥BD ，∴四边形 AGBD 是平行四边形．

∵四边形 BEDF 是菱形，

∴DE＝BE ．∵AE＝BE ，

∴AE＝BE＝DE ．

∴∠1＝∠2，∠3＝∠4．

∵∠1+∠2+∠3+∠4＝180°，∴2∠2+2∠3＝180°．

∴∠2+∠3＝90°．

即∠ADB＝90°．

∴四边形AGBD是矩形．

课时三正方形

9. □AFCE是菱形，△AOE≌△COF，四边形AFCE是平行四边形，EF⊥AC

8.四边形AEDF是菱形，∵DE∥AC，∴∠ADE＝∠DAF，

∵AD是△ABC的角平分线，

∴∠DAE＝∠DAF，∴∠ADE=∠DAE，∴AE=ED.

又∵DE∥AC，DF∥AB

∴四边形AEDF是平行四边形，∴平行四边形AEDF是菱形.

1. B；2. C; 3.答案不唯一：等；4.5；5.C；6.24，提示：由已知得菱形一边长为5，由菱形的对角线互相平分且垂直，所以另一条对角线的长为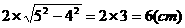，∴S_菱=；7.①②⑥或③④⑤或③④⑥；