3.把两个全等的非等腰三角形拼成平行四边形，可拼成的不同平行四边形的个数为(　　　 )

A.1　　 B.2　　 C.3　　 D.4

2.已知：四边形ABCD中，AD∥BC，分别添加下列条件之一：①AB∥CD；② AB=CD, ③AD=BC，④∠A=∠C，⑤∠B=∠D，能使四边形ABCD成为平行四边形的条件的个数是(　　 )

A.4　　　 B.3　　 C.2　　 D.1

1.下列条件中不能判定四边形ABCD为平行四边形的是(　　　　 )

A.AB=CD,AD=BC　　　　　　　 B.AB∥CD，AB=CD

C.AB=CD ，AD∥BC　　　　　　 D. AB∥CD，AD∥BC

12. 解：(1)有4对全等三角形．　　

　　 分别为△AMO≌△CNO，△OCF≌△OAE，△AME≌△CNF，△ABC≌△CDA．

　　 (2)证明：∵OA=OC，∠1=∠2，OE=OF，

　　 ∴△OAE≌△OCF，∴∠EAO=∠FCO．　

　　 在ABCD中，AB∥CD，

∴∠BAO=∠DCO，∴∠EAM=∠NCF．　　

课时三平行四边形的判定(一)

11.证明：∵DE∥AB，DF∥AC

∴四边形AEDF是平行四边形，∴DF=AE，又∵DE∥AB，∴∠B=∠EDC，又∵AB=AC,∴∠B=∠C，∴∠C=∠EDC，∴DE=CE，∴DF+DE=AE+CE=AC=AB.

7.D，提示：因为平行四边形的对角线把平行四边形分成面积相等的4个小三角形，所以平行四边形的面积为4；8.C，提示：根据三角形的两边之和大于第三边，两边之差小于第三边，若，则，所以符合条件的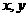可能是18与20；9.30；10.8;

6. OE=OF,　 在□ABCD中，OB=OD，∵BE⊥AC，DF⊥AC∴∠BEO＝∠DFO，

又∠BOE＝∠DOF，∴△BOE≌△DOF，∴OE=OF.

5. 证明：∵ABCD,∴OA=OC,DF∥EB∴∠E=∠F,又∵∠EOA=∠FOC

∴△OAE≌△OCF,∴OE=OF；

1. 10＜x＜22，提示：根据三角形的三边关系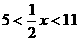得，解得；2. B；3. BC=AD=4.8；4.A；提示：根据面积法求出邻边的比为3∶2，则邻边为7.5，5，则面积为7.5×2=15²　 ；

12. 如图，□ABCD O为D的对角线AC的中点，过点O作一条直线分别与AB、CD交于点M、N，点E、F在直线MN上，且OE=OF．

(1)图中共有几对全等三角形，请把它们都写出来；

(2)求证：∠MAE=∠NCF．

课时二答案：