7．下列命题的逆命题为真命题的是(　 )

　　 A．如果a=b，那么a²=b²　　　 B．平行四边形是中心对称图形

　　 C．两组对角分别相等的四边形是平行四边形　　 D．内错角相等

6．下列说法中，正确的是(　 )

　　 A．每一个命题都有逆命题　　 B．假命题的逆命题一定是假命题

　　 C．每一个定理都有逆定理　　 D．假命题没有逆命题

5．命题“对顶角相等”的逆命题是_____________________，是_____命题．

[基础过关]

4．线段垂直平分线性质定理的逆定理是_____________________．

3．每个命题都有它的________，但每个真命题的逆命题不一定是真命题．

2．如果一个定理的逆命题能被证明是真命题，那么就叫它是原定理的________，这两个定理叫做_________．

1．在两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论是第二个命题的条件，那么这两个命题叫做________．

5.7 逆命题和逆定理(1)同步练习

[知识盘点]

2．出入相补原理是我国著名数学家吴文俊先生提出的，他认为这个原理“就是指这样的明显事实:一个平面图形从一处移到他处，面积不变．又若把图形分割成若干块，那么各部分面积的和等于原来图形的面积，因而图形移置前后诸面积间的和、差有简单的相等关系．立体的情形也是如此”．

我们教材中介绍的勾股定理的证明就用到了出入相补原理．

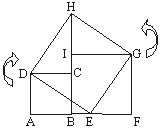
下面我们再介绍刘徽的一种证明勾股定理的方法:如图，正方形ABCD、BFGI的边长分别为b、a，在BF上取一点E，使AE=a，连结DE、GE，将△ADE移至△CDH，将△EFG移至△HIG，由此就可以证明勾股定理，你试一试吧!

1．在中，，，边上的高，试求的长．