5．若正方形的一条对角线长为a，则这个正方形的面积是______．

4．若一个四边形有四条对称轴，则这个四边形是______．

3．判定一个四边形是正方形除根据定义判别外，通常还有如下方法：

　　 (1)有一组邻边相等的_________是正方形；

　　 (2)有一个角是直角的________是正方形．

2．正方形既是特殊的________，又是特殊的_________，所以它同时具有______和________的性质．

　 (1)正方形的四个角_______，四条边________；

　 (2)正方形的对角线_____，并且_________，每条对角线平分_________．

1．我们把有一组邻边_______，并且有一个角是_______的_________的叫做正方形．

6.3 正方形 同步练习

[知识盘点]

5．已知CD为一幅3m高的温室外墙，其南面窗户的底框G距地面1m，且CD在地面上留下的影长CF为2m，现欲在距C点7m的正南方A点处建一幢12m高的楼房AB(设A、C、F在同一水平线上)．

　 (1)按比例较精确地画出高楼AB及它的影长AE；

(2)楼房AB建成后是否影响温室CD的采光？试说明理由．

[后花园]

　　 妙趣角　　　 相似三角形的古老应用

　　 相似三角形的运用在我国有着非常久远的历史，在国际数学界也起到了引领的作用．

　　 我们的祖先很早就知道利用相似直角三角形的性质来进行测量．我国最早运用于测量的工具是“矩形”．约在公元前1100年，商高便精通使用矩尺测量的方法，并提出了可以利用矩形和三角形相似的原理进行测量．

　　 商高说：“偃矩以望高，覆矩以测深，卧矩以知远．”

　　 第一句话用图来说明，由于△ANP∽△ACB，显然可知高NP=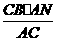．第二句话的意思是，如果把直尺CB倒垂过来，就可以测量深处的目标的尺度．第三句话的意思是，如果把直尺CB平卧放在水平面上，就可以测量远处两目标间的尺度．由此可知，适当应用矩尺，便可测量出许多目标的高、深、广、远，因此商高总结说：“智出于句，句出于矩”．

　　 三国时魏国数学家刘徽进一步解决了下列9种测量问题：

　　 (1)从海上测量岛屿的高度；(2)测量山上的树高；(3)测量远处一个有城墙的城市的大小；(4)测量涧谷的深度；(5)从山上测量平地上塔的高度；(6)在地面测量远处河口的宽度；(7)测量透明水池的深度；(8)从山上测河宽；(9)从山上测量城市的大小．

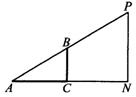
4．课外实习小组想利用树影测量树高，他们在同一时刻测得一身高为1.5m的同学的影长为1.35m，因大树靠近一幢建筑物，影子不全在地面上(如图)，现测得地面上树影的长BC=3.6m，墙面上树影的高CD=1.8m，求树高AB的长．

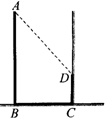
3．如图，在某一时刻竖立在操场上的竹竿AB的影长为BC，请据此在图上画出操场上的树MN在此时的影长(用线段表示)．

[拓展与延伸]

2．某一时刻，小刚测得竖立于地面上的1m长的木尺的影长为0.8m，此刻学校25m高的教学楼的影长是________m．