
题目列表(包括答案和解析)
11. 2三角形全等的判定(二)
2三角形全等的判定(二)
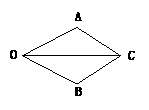
2. 如图,已知图中有两对三角形全等,填空:
如图,已知图中有两对三角形全等,填空:
(1)△ABM≌ ,在这两个全等三角形中,AB的对应边是 ,BM的对应边是 ,MA的对应边是 ;
(2)△ABN≌ ,在这两个全等三角形中,∠BAN的对应角是 ,∠B的对应角是 ,∠ANB的对应角是 .
1.填空:
(1)能够完全 的两个三角形叫做全等三角形;
(2)把两个全等三角形重合到一起,重合的顶点叫做 ,重合的边叫做 ,重合的角叫做 ;
 (3)全等三角形的
相等,全等三角形的
相等.
(3)全等三角形的
相等,全等三角形的
相等.
11.2三角形全等的判定(一)
3.4《三角形全等的判定定理》同步练习
第1题. 如图, 中,
中,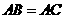 ,
, ,则由“
,则由“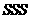 ”可以判定( )
”可以判定( )
A. B.
B.
 C.
C. D.以上答案都不对
D.以上答案都不对
答案:B
第2题. 如图, 中,
中,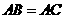 ,
,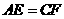 ,
, ,则
,则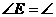 ________,
________,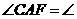 __________.
__________.

答案: ,
,
第3题. 如图, ,
,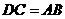 ,
,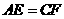 ,找出图中的一对全等三角形,并说明你的理由.
,找出图中的一对全等三角形,并说明你的理由.

答案:答案不惟一.如 .理由:根据“
.理由:根据“ ”即
”即 ,
, ,
, .
.
第4题. 如图, 是等边三角形,若在它边上的一点与这边所对角的顶点的连线恰好将
是等边三角形,若在它边上的一点与这边所对角的顶点的连线恰好将 分成两个全等三角形,则这样的点共有( )
分成两个全等三角形,则这样的点共有( )
A.1个 B.3个 C.6个 D.9个

答案:B
第5题. 如图,已知 ,
, .求证:
.求证: .
.

答案:在 和
和 中
中
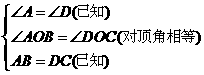
 .
.
第6题. 如图,点 分别在
分别在 上,且
上,且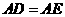 ,
,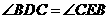 .
.
求证: .
.

答案: ,
, ,
,
又


 ,即
,即 .
.
 第7题. 已知
第7题. 已知 交
交 ,垂足为
,垂足为 ,
, ,
, .
.
求证:(1)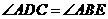 ;
;
(2) .
.
答案:(1) ,
, 又
又
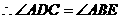
(2)在 和
和 中
中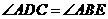 (已证),
(已证), (已知),
(已知),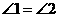 (已知)
(已知)
 .
.
第8题. 如图,已知 为等边三角形,
为等边三角形, ,垂足为
,垂足为 ,
,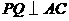 ,垂足为
,垂足为 ,
, ,垂足为
,垂足为 ,且
,且 .
.
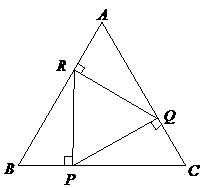 求证:
求证: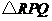 为等边三角形.
为等边三角形.
答案: 是等边三角形.
是等边三角形. ,
,
又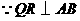 ,
,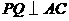 ,
,

又 ,根据
,根据 证
证
得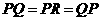
 为等边三角形.
为等边三角形.
第9题. 如图,已知点 在
在 上,
上, ,
, ,
, .
.
 求证:
求证: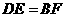 .
.
答案:由 得
得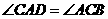 ,根据等角的补角相等得
,根据等角的补角相等得 ,又由
,又由 得
得 ,又
,又 ,根据
,根据 证
证 得
得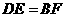 .
.
第10题.  如图,在
如图,在 和
和 中,已知
中,已知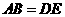 ,
, ,根据(SAS)判定
,根据(SAS)判定 ,还需的条件是( )
,还需的条件是( )
A.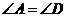
B.
C.
D.以上三个均可以
答案:B
第11题. 若按给定的三个条件画一个三角形,图形惟一,则所给条件不可能是( )
A.两边一夹角 B.两角一夹边 C.三边 D.三角
答案:D
第12题.  如图,已知
如图,已知 ,垂足为
,垂足为 ,
,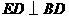 ,垂足为
,垂足为 ,
, ,
, ,则
,则 =___________
=___________ .
.
答案: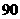
第13题. 如图,已知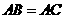 ,
,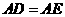 ,
, .
.
 求证:
求证: .
.
答案:先证 ,再根据
,再根据 证
证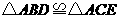 ,得
,得 .
.
第14题. 下列各命题中,真命题是( )
A.如果两个三角形面积不相等,那么这两个三角形不可能全等
B.如果两个三角形不全等,那么这两个三角形面积一定不相等
C.如果 ,
, ,那么
,那么 与
与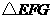 的面积的和等于
的面积的和等于 与
与 面积的和
面积的和
D.如果 ,
, ,那么
,那么
答案:A
 第15题. 如图,已知
第15题. 如图,已知 ,
, ,
, .
.
求证: .
.
答案:先证: ,再根据
,再根据 证
证 ,得
,得 .
.
第16题. 如图,点 是
是 的平分线上的一点,作
的平分线上的一点,作 ,垂足为
,垂足为 ,
, 垂足为
垂足为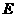 ,
, 交
交 于点
于点 .
.
(1)你能找到几对全等三角形?请说明理由;
(2)你能确定图中共有几个直角吗?请说明理由.

答案:(1)有三对全等三角形.由“ ”可知
”可知 ,又由“
,又由“ ”可知:
”可知: ,
,
(2)共有八个直角,由(1)中的 可知:
可知: ,而
,而 ,因此
,因此 .这样以
.这样以 为顶点有四个直角,另有已知的四个直角,共计八个直角.
为顶点有四个直角,另有已知的四个直角,共计八个直角.
第17题. 如图,已知 ,
, ,
, 是
是 中点,过
中点,过 作直线交
作直线交 的延长线于
的延长线于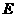 ,交
,交 的延长线于
的延长线于 .
.
求证: .
.

答案:在 和
和 中,
中,


 (全等三角形对应角相等)
(全等三角形对应角相等)
 是
是 中点,
中点,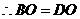


 .
.
第18题. 如图,已知 ,
, ,
, .
.
 求证:
求证: .
.
答案:

 又
又 ,
, ,根据“
,根据“ ”证
”证 .
.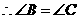 ,又
,又 ,
, ,根据
,根据 证
证
 .
.
第19题. 对于下列各组条件,不能判定 的一组是( )
的一组是( )
A. ,
,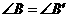 ,
,
B. ,
, ,
,
C. ,
, ,
,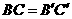
D. ,
, ,
,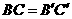
答案:C
第20题. 如图,把两根钢条 ,
,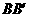 的中点
的中点 连在一起,可以做成一个测量工件内槽宽的工具(工人把这种工具叫卡钳)只要量出
连在一起,可以做成一个测量工件内槽宽的工具(工人把这种工具叫卡钳)只要量出 的长度,就可以知道工件的内径
的长度,就可以知道工件的内径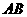 是否符合标准,你能说出工人这样测量的道理吗?
是否符合标准,你能说出工人这样测量的道理吗?

答案:此工具是根据三角形全等制作而成的.由 是
是 ,
,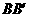 的中点,可得
的中点,可得 ,
, ,又由于
,又由于 与
与 是对顶角,可知
是对顶角,可知 ,于是根据“
,于是根据“ ”有
”有 ,从而
,从而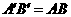 ,只要量出
,只要量出 的长度,就可以知道工作的内径
的长度,就可以知道工作的内径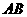 是否符合标准.
是否符合标准.
第70题. 如图,已知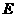 是等边
是等边 内一点,
内一点, ,
, 是
是 外的一个点,
外的一个点, ,
, .
.
 求证:
求证: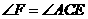 .
.
答案:先根据 证明
证明
 ,
, ,又
,又 是等边三角形
是等边三角形
 ,又
,又 ,
, ,根据
,根据 证
证 .
.
第21题. 如图,已知在 和
和 中,
中, 与
与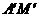 分别是
分别是 上的中线,
上的中线, ,
, ,
, .
.
求证: .
.

答案:延长 到
到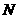 使
使 ,延长
,延长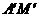 至
至 使
使
 ,连接
,连接 ,
, 先证
先证 ,得
,得 ,
, 同理可证
同理可证 ,
, .利用
.利用 证
证 .
. ,
, .
.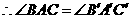 ,根据
,根据 证
证 .
.
第22题. 如图,已知在 中,
中,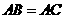 ,
,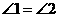 .
.
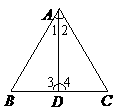 求证:
求证: ,
,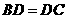 .
.
答案:在 和
和 中,
中,

 .
.
 ,
, .
.
又 ,即
,即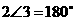 ,
, ,
, .
.
第23题. 如图,平面内有一个 ,
, 为平面内的一点,延长
为平面内的一点,延长 到
到 ,使
,使 ,延长
,延长 到
到 ,使
,使 ,延长
,延长 到
到 ,使
,使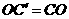 ,得到
,得到 ,
, 与
与 是否全等?这两个三角形的对应边是否平行?为什么?
是否全等?这两个三角形的对应边是否平行?为什么?

答案: ,
, ,
, ,
, ,理由略.
,理由略.
第24题. 如图,在 中,
中, ,
, 分别为
分别为 上的点,且
上的点,且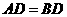 ,
,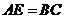 ,
,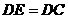 .
.
 求证:
求证: .
.
答案:在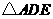 和
和 中,
中,


第25题. 如图,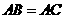 ,要使△
,要使△ △
△ ,应添加的条件是 ,(添加一
,应添加的条件是 ,(添加一 个条件即可)
个条件即可)
答案:答案不惟一,如 等.
等.
第26题. 如图,四边形 中,
中, 垂直平分
垂直平分 ,垂足为点
,垂足为点 .
.
 (1)图中有多少对全等三角形?请把它们都写出来;
(1)图中有多少对全等三角形?请把它们都写出来;
(2)任选(1)中的一对全等三角形加以证明.

答案:解:(1)图中有三对全等三角形:
△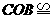 △
△ ,△
,△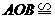 △
△ ,△
,△ △
△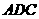 .
.
(2)证明△ △
△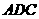 .
.
证明: 垂直平分
垂直平分 ,
,
 ,
, .
.
又 ,
, △
△ △
△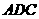 .
.
第27题. 在△ △
△ 中,已知
中,已知 ,
, ,要判定这两个三角形全等,还需要条件( )
,要判定这两个三角形全等,还需要条件( )
A. B.
B. C.
C. D.
D.
答案:C
第28题. 小明用四根竹棒扎成如图所示的风筝框架,已知 ,
, ,你认为小明的风筝两脚大小相同吗(即
,你认为小明的风筝两脚大小相同吗(即 ,
, 相等吗)?请说明理由.
相等吗)?请说明理由.

答案:相等.可以连接 ,由
,由 可知
可知

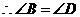 .
.
第29题. 小民用五根木条钉成了如图所示的两个三角形,且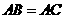 ,
, ,若
,若 为锐角三角形,则
为锐角三角形,则 中的最大角
中的最大角 的取范围是( )
的取范围是( )
 A.
A.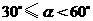 B.
B.
C. D.
D.
答案:D
第30题. 已知: 的三边分别为
的三边分别为 ,
, 的三边分别为
的三边分别为 ,且有
,且有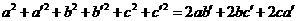 ,则
,则 与
与 ( )
( )
A.一定全等 B.不一定全等 C.一定不全等 D.无法确定
答案:A
第31题.  如图,已知
如图,已知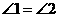 ,
, .
.
求证: .
.
答案: ,
, ,
,
又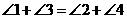
即 ,
,
又 根据
根据 证
证 ,
,
 .
.
第32题.  你见过形如图所示的风筝吗?开始制作时,
你见过形如图所示的风筝吗?开始制作时, ,
, ,后来为了加固,又过点
,后来为了加固,又过点 加了一根竹棒
加了一根竹棒 ,分别交
,分别交 于点
于点 ,且
,且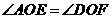 ,你认为
,你认为 相等吗?请说明理由.
相等吗?请说明理由.
答案:相等.可以连接 ,首先由“
,首先由“ ”可知:
”可知: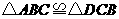 ,因此
,因此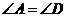 ,同理可得
,同理可得 ,又由“
,又由“ ”可知
”可知 ,因此
,因此 .最后可由“
.最后可由“ ”得
”得 ,所以
,所以 .
.
第33题. 如图, 相交于点
相交于点 ,
,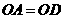 ,
, .
.
求证: .
.

答案:在 和
和 中,
中,
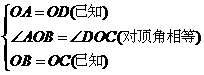
 .
.
第34题. 如图,已知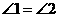 ,
, ,
, .
.
求证: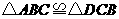 .
.

答案:: ,
,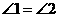 ,
, ,即
,即 ,又
,又 ,
, ,
, ,
,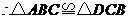 .
.
第35题. 在 和
和 中,①
中,① ;②
;②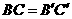 ;③
;③ ;④
;④ ;⑤
;⑤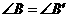 则下列条件中不能保证
则下列条件中不能保证 的是( )
的是( )
A.①②③ B.①②⑤ C.②④⑤ D.①③⑤
答案:D
第36题. 在 和
和 中,已知
中,已知 ,
, ,在下列说法中,错误的是( )
,在下列说法中,错误的是( )
A.如果增加条件 ,那么
,那么 (
( )
)
B.如果增加条件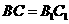 ,那么
,那么 (
( )
)
C.如果增加条件 ,那么
,那么 (
( )
)
D.如果增加条件 ,那么
,那么 (
( )
)
答案:B
第37题.  如图,
如图, 与
与 交于点
交于点 ,
, 相等吗?为什么?
相等吗?为什么?
答案:不一定. 与
与 可能相等,也可能不相等.
可能相等,也可能不相等.
直观地解释: 上的位置不定,因此
上的位置不定,因此 的关系也不定.
的关系也不定.
逻辑地解释: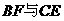 所在的两个三角形,无法确定其是否全等,因此
所在的两个三角形,无法确定其是否全等,因此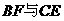 的关系不一定.
的关系不一定.
 第38题. 如图,
第38题. 如图,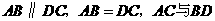 相交于点
相交于点 ,你能找出两对全等的三角形吗?你能说明其中的道理吗?
,你能找出两对全等的三角形吗?你能说明其中的道理吗?
答案:事实上有四对全等的三角形.
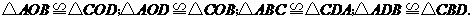
理由分别是:
 的理由:“角边角”,即
的理由:“角边角”,即
 的理由.“边角边”,即
的理由.“边角边”,即
 的理由:“边角边”.即
的理由:“边角边”.即
 的理由:“边角边”.即
的理由:“边角边”.即
第39题. 已知:如图, 是△
是△ 的边
的边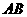 上一点,
上一点, ,
, ,
, .
.

 .
.
答案:证明: ,
,
 .
.
又 ,
, ,
,
 △
△ △
△ .
.

 .
.
第40题. 如图,给出五个等量关系:① 、②
、② 、③
、③ 、④
、④ 、⑤
、⑤ .
.
<
10.直角三角形中,一个锐角等于另一个锐角的5倍,这个锐角的度数是 _________.
[ ]
A.15° B.75° C.45° D.90°
9.在△ABC中,∠A:∠B:∠C=1:2:1,则△ABC为 _________.
[ ]
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
8.若△ABC的三个内角A,B,C满足,3∠A=5∠B,3∠C=2∠B,则这个三角形是 _________.
[ ]
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定
7.三个角不相等的三角形中,它的最小角α的范围是 _________.
[ ]
A.0°<α<30° B.0°<α<45°
C.0°<α<60° D.0°<α<90°
6.在△ABC中,∠A=105°,∠B-∠C=15°,则∠C的度数为 _________.
[ ]
A.15° B.30°
C.45° D.90°
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com