
题目列表(包括答案和解析)
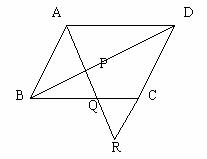
5. 如图平行四边形ABCD中,过A作直线交BD于P,交BC于Q,交DC的延长线于R,求证:AP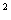 =PQ·PR
=PQ·PR
4. 正方形ABCD中,E为CD的中点,F在BC上,且CF∶BC=1∶4,求证: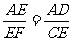
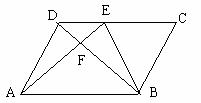
3. 如图,平行四边形ABCD中,E在CD上,DE:CE=2:3连AE、BE、BD且AE、BD相交于点F,则SΔDEF:SΔEBF:SΔABF为( )
A. 4∶10∶25 B. 4∶9∶25 C. 2∶3∶5 D. 2∶5∶25
2. 两个相似三角形的面积之比为9:4,若较大三角形的一个内角的平分线长6cm,则另一个三角形对应角的平分线长为_________
1. ΔABC中,D、E分别为AB、AC的中点,连DE则ΔADE与ΔABC的周长之比为________; 它们的面积之比为________
2.6相似三角形的性质同步练习
[典型例题]
例1. 如图,AB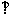 BC
, CD
BC
, CD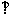 BC, B,C是垂足,AC,BD交于P。过P作PQ
BC, B,C是垂足,AC,BD交于P。过P作PQ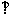 BC于Q。
BC于Q。
求证: AQP=
AQP= PQD
PQD
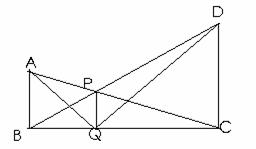
分析:由已知AB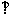 BC
, CD
BC
, CD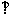 BC,PQ
BC,PQ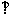 BC,则AB‖PQ‖DC
BC,则AB‖PQ‖DC
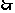
 AQP=
AQP= QAB,
QAB,  PQD=
PQD= QDC
QDC
又已知Rt ABQ和Rt
ABQ和Rt DCQ
DCQ
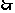 只须证明Rt
只须证明Rt ABQ∽Rt
ABQ∽Rt DCQ即可
DCQ即可
证明: AB‖PQ‖DC
AB‖PQ‖DC
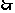
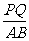 ==
==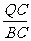 ,
,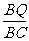 =
=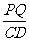
∴PQ·BC=AB·CQ=CD·BQ
∴AB·CQ=CD·BQ 即 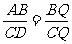
又ΔABQ ,ΔDCQ均为直角三角形
∴RtΔABQ∽RtΔDCQ
∴∠BAQ=∠CDQ ∴∠AQP=∠PQD
例2. 如图,ΔACB中,∠ACB=90º,D在BC边上,连AD,过B作BE⊥AB,∠BAE=∠CAD,过E作EF⊥CB于F
求证:BF=CD
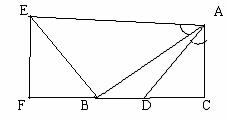
分析:∠C=∠EBA=90º,∠BAE=∠CAD
∴RtΔACD∽RtΔABE
又易知∠ABC与∠FBE互余,且∠C=∠F=90º
∴RtΔACB∽RtΔBEF
∴只须寻找与线段AB,BE“相关”的比例式即可
证明:RtΔACD与RtΔABE中,
∵∠CAD=∠BAE
∴RtΔACD∽RtΔABE
∴
∴CD=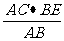 … ①
… ①
又BE⊥AB,BF⊥AC ∵∠FBE=∠CAB
∴RtΔACB∽RtΔBFE
∴ ∴BF=
∴BF=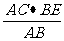 … ②
… ②
∴由①②知:BF=CD
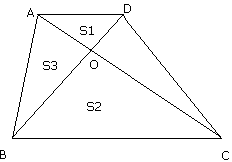
例3. 如图,梯形ABCD中,AD//CB 对角线AC,BD相交于点O,设梯形ABCD的面积为S,ΔAOD,ΔBOC,ΔAOB的面积分别为S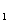 ,S
,S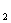 和S
和S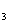
证明: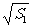 ,
, 是方程X
是方程X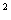 -
- X+
S
X+
S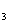 =0的两实数根
=0的两实数根
分析:本题实质上是证明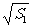 +
+ =
= 且
且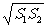 = S
= S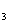 ,即已知S
,即已知S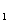 ,S
,S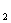 ,求S
,求S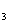 和S,由相似三角形和同底上三角形的面积比的性质,将面积比转换为线段之比即可
和S,由相似三角形和同底上三角形的面积比的性质,将面积比转换为线段之比即可
证明: ∵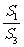 =
=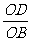 ,
,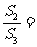
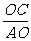
∴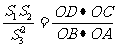
∵AD//BC ∴
ΔAOD∽ΔCOB ∴
∴ =1
=1
∴S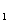 S
S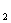 =
= ,即
,即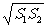 = S
= S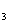 … ①
… ①
又S= S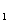 +S
+S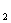 +2S
+2S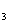 =
S
=
S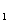 +2
+2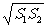 +
S
+
S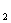 =(
=(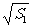 +
+ )
)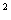
∴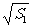 +
+ =
= … ②
… ②
∴由①②可知,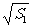 ,
, 是方程X
是方程X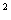 -
- X+
S
X+
S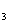 =0的两个实数根
=0的两个实数根
[模拟试题]
12.如图,在Rt△ABC中,∠BCA=90°,CD是高,已知Rt△ABC的三边长都是整数且BD=113,求Rt△BCD与Rt△ACD的周长之比.
11.如图,已知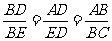 ,求证:△ABC∽△DBE.
,求证:△ABC∽△DBE.
◆拓展训练
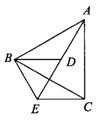
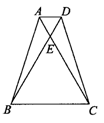
10.如图所示,梯形ABCD中,AD∥BC,AB=CD,∠ADB=60°,BD=10,DE:EB=1:4,求梯形的面积.
9.如上右图,已知矩形ABCD中,AB=10,BC=12,E为DC中点,AF⊥BE于点F,则AF=_____.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com