23、某人从A城出发，前往离A城30千米的B城。现在有三种车供他选择：①自行车，其速度为15千米/时；②三轮车，其速度为10千米/时；③摩托车，其速度为40千米／小时。

(1)用哪些车能使他从A城到达B城的时间不超过2小时，请说明理由。

(2)设此人在行进途中离B城的路程为s千米，行进时间为小时，就(1)所选定的方案，试写出s与t的函数关系式(注明自变量t的取值范围):　　　　　　　　　　

(3)在图7所给的平面直角坐标系中画出此函数的图像。

22、某通讯移动通讯公司手机费用有A、B两种计费标准，如下表：

设某用户一个月内手机通话时间为x分钟，请根据上表解答下列问题：(1)按A类收费标准，该用户应缴纳y₁=　　　　　　 元；按B类收费标准，该用户应缴纳y₁=　　　　　　 元；(用含x的代数式表示)(2)如果该用户每月通话时间为300分钟，应选择哪种收费方式？(3)如果该用户每月手机费用不超过90元，应选择哪种收费方式？

20、如图，矩形OABC中，O为直角坐标系的原点，A、C两点的坐标分别为(3，0)、(0，5)。

(1)直接写出B点坐标；

(2)若过点C的直线CD交AB边于点D，且把矩形OABC的周长分为1∶3两部分，求直线CD的解析式；

19、某公司到果园基地购买某种优质水果，慰问医务工作者，果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案，甲方案：每千克9元，由基地送货上门。乙方案：每千克8元，由顾客自己租车运回，已知该公司租车从基地到公司的运输费为5000元。

(1)分别写出该公司两种购买方案的付款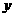(元)与所购买的水果质量(千克)之间的函数关系式，并写出自变量的取值范围。

(2)依据购买量判断，选择哪种购买方案付款最少？并说明理由。

18、宁安市与哈尔滨市两地相距360千米.甲车在宁安市，乙车在哈尔滨市，两车同时出发，相向而行，在A地相遇.为节约费用(两车相遇并换货后，均需按原路返回出发地)，两车换货后，甲车立即按原路返回宁安市.设每车在行驶过程中速度保持不变，两车间的距离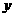(千米)与时间(小时)的函数关系如图所示.根据所提供的信息，回答下列问题：

⑴甲车的速度:　　　　　　　 　;乙车的速度:　　　　　　 　;

⑵说明从两车开始出发到5小时这段时间乙车的运动状态.

17、某公司市场营销部的营销员的个人月收入与该营销员每月的销量成一次函数关系，其图象如图所示. 根据图象提供的信息，解答下列问题：

(1)求出营销人员的个人月收入y元与该营销员每月的销售量x万件(x≥0)之间的函数关系式:

(2)已知该公司营销员李平5月份的销售量为1.2万件，求李平5月份的收入.

16、某地电话拨号入网有两种收费方式，用户可以任选其一：

(A)　　　 计时制：0.05元/分；　 (B) 包月制：50元/月(限一部个人住宅电话上网)．

此外，每一种上网方式都得加收通信费0.02元/分．

(1)请你分别写出两种收费方式下用户每月应支付的费用y(元)与上网时间x(小时)之间的函数关系式: 计时制：　　　　　　　　　　 包月制：　　　　　　　

(2)　 若某用户估计一个月内上网的时间为20小时，你认为采用哪种方式较为合算？

15、在某地，人们发现某种蟋蟀1分钟所叫次数与当地温度之间近似为一次函数关系。下面是蟋蟀所叫次数与温度变化情况对照表：

　 (1)根据表中数据确定该一次函数的关系式；

　 (2)如果蟋蟀1分钟叫了63次，那么该地当时的温度大约为多少摄氏度？

14、如图15-1和15-2，在20×20的等距网格(每格的宽和高均是1个单位长)中，Rt△ABC从点A与点M重合的位置开始，以每秒1个单位长的速度先向下平移，当BC边与网的底部重合时，继续同样的速度向右平移，当点C与点P重合时，Rt△ABC停止移动.设运动时间为x秒，△QAC的面积为y.

(1)如图15-1，当Rt△ABC向下平移到Rt△A₁B₁C₁的位置时，请你在网格中画出Rt△A₁B₁C₁关于直线QN成轴对称的图形；

(2)如图15-2，在Rt△ABC向下平移的过程中，请你求出y与x的函数关系式，并说明当x分别取何值时，y取得最大值和最小值？最大值和最小值分别是多少？

(3)在Rt△ABC向右平移的过程中，请你说明当x取何值时，y取得最大值和最小值？最大值和最值分别是多少？为什么？