5．如果梯形的中位线长为9cm，下底的长为12cm，那么这个梯形的上底的长等于_________cm．

4．在梯形ABCD中，AD∥BC，已知∠B=25°，∠C=75°，则∠A=______，∠D=_____．

3．如图3，在等腰梯形ABCD中，AD=2cm，BC=4cm，高DF=2cm，则DC=_______cm．

2．如图2，在梯形ABCD中，AD∥BC，两对角线交于点O，则图中面积相等的三角形有(　 )．

(A)4对　　 (B)3对　　 (C)2对　　 (D)1对

1．如图1，在等腰梯形ABCD中，AD∥BC，AD=5，AB=6，BC=8，且AB∥DE，则△DEC的周长是(　 )．

(A)3　　　 (B)12　　 (C)15　　 (D)19

　　 (1)　　　　　　　　　　　 (2)　　　　　　　　　　 (3)

6.4 梯形(1)同步练习

解题示范

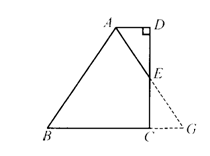例　 如图，在梯形ABCD中，AD∥BC，DC⊥AD．AE平分∠BAD交CD于点E，且DE=EC．求证：AB=AD+BC．

　　 审题　 本题是在梯形ABCD中证明线段的和差问题，提供的条件也较为丰富，如AD∥BC，DC⊥AD，AE平分∠BAD，且DE=EC，因此运用全等三角形不难解决此题．

　　 方案　 延长AE，BC相交于点G，从而构造了△ADE≌△GCE，得AD=CG．由AE平分∠BAD，可得∠DAE=∠BAE．由AD∥BC，可得∠DAE=∠G．于是∠BAE=∠G，得到AB=BE．通过等量代换得AB=BC+CG=BC+AD．

　　 实施　 延长AE，BC相交于点G．

　　 ∵AD∥BC，∴∠DAE=∠G．

　　 ∵∠DAE=∠BAE，∴∠BAE=∠G．∴AB=BG．

　　 在△ADE和△GCE中，∵∠DAE=∠G，∠AED=∠GEC，DE=EC，

　　 ∴△ADE≌△GCE，∴AD=CG．

　　 ∵AB=BC+CG，∴AB=BC+AD．

　　 反思　 本题采用“补短”的方法解决线段和的问题，这是证明线段和差问题的常用方法，即把短线段BC补一段CG，使CG=AD，这样问题就转化成证明BG=AB．本题也可以用“截长法”来处理，过点E作AB的垂线段，即把长线段AB截成两段，证明其中一段等于AD，再证余下的一段等于BC．同学们不妨试一试．

课时训练

7．在梯形ABCD中，AD∥BC，∠B=90°，AB=14cm，AD=18cm，BC=21cm，点P从点A开始沿AD边向点D以1cm/s的速度移动，点Q从点C开始沿CB向点B以2cm/s的速度移动．如果点P，Q分别从点A，C同时出发，设移动时间为xs时，梯形PQCD刚好是等腰梯形，过点D作DE⊥BC，垂足为E，过点Q作QF⊥AD，垂足为F．求x的值．

6．两条对角线相等的梯形是等腰梯形吗？如果是，请你写出已知、求证、并加以证明．

　　 已知：

　　 求证：

证明：

5．已知：如图，在四边形ABCD中，∠A与∠B互补，∠A与∠C互补，AD≠BC．求证：四边形ABCD是等腰梯形．

4．在梯形ABCD中，AD∥BC，对角线AC，BD相交于点O，∠ABD=∠DCA，∠DBC=∠ACB．梯形ABCD是等腰梯形吗？说说你的理由．