12. 所谓的勾股数就是指使等式a²+b²=c²成立的任何三个自然数。我国清代数学家罗士林钻研出一种求勾股数的方法，即对于任意正整数m、n(m＞n)，取a=m²-n²，b=2mn，c=m²+n²，则a、b、c就是一组勾股数。请你结合这种方法，写出85(三个数中最大)、84和　　　　 组成一组勾股数。

11. 一艘轮船以16海里/时的速度离开港口向东南方向航行，另一艘轮船在同时同地以12海里/时的速度向西南方向航行，则一个半小时后两船相距　　　　 海里。

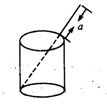
9. 如图，将一根长24cm的筷子，置于底面直径为5cm，高为12cm的圆柱形茶杯中，设筷子露在杯子外面的长为acm(茶杯装满水)，则a的取值范围是　　　　　　　　　 。

　 10. 如图，数轴上有两个Rt△ABC、Rt△ABC，OA、OC是斜边，且

OB=1，AB=1，CD=1，OD=2，分别以O为圆心，OA、OC为半径

画弧交x轴于E、F，则E、F分别对应的数是　　　　　　　　　　 。

7. 已知一个直角三角形的两边长分别是3和4，则第三边长为　　　　　 。

　 　 8. 如图所示，在矩形ABCD中，AB=16，BC=8，将矩形沿AC折叠，点D落在点E处，且CE与AB交于点F，那么AF=　　　　 。

6. 在Rt△ABC中，∠C=90°，若a:b=3:4，c=20，则a=　　 ，b=　　 。

5. 飞机在空中水平飞行，某一时刻刚好飞到小刚头顶正上方4000米处，过了20秒，飞机距离小刚5000米，则飞机每小时飞行　　　　　 千米。

4. 三角形中两边的平方差恰好等于第三边的平方，则这个三角形是　　　 三角形。

3. 把直角三角形的两条直角边同时扩大到原来的2倍，则其斜边扩大到原来的　　　　　 。

　 1. 如图，在长方形ABCD中，已知BC=10cm，AB=5cm，则对角线BD=　　　　　 cm。

2. 如图，在正方形ABCD中，对角线为2，

则正方形边长为　　　　 。

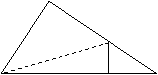例4：如图3，在△ABC中，∠C=90º，D是AC的中点，DE⊥AB于E点，试说明：BC²=BE²－AE²。

析解：由于要说明的是线段平方差问题，故可考虑利用勾

股定理，注意到∠C=∠BED=∠AED=90º及CD=AD，可连结

BD来解决。因为∠C=90º，所以BD²=BC²+CD²。又DE⊥AB，

所以∠BED=∠AED=90º，在Rt△BED中，有BD²=BE²+DE²。在Rt△AED中，有AD²= DE²+AE²。又D是AC的中点，所以AD=CD。故BC²+CD²= BC²+ A D²= BC²+ DE²+AE²= BE²+ DE²，所以BE²= BC²+ AE²，所以BC²=BE²－AE²。

点评：若所给题目的已知或结论中含有线段的平方和或平方差关系时，则可考虑构造直角三角形，利用勾股定理来解决问题。