2、(10分)一玩具厂生产甲、乙两种玩具，已知造一个甲种玩具需用金属80克，塑料140克，造一个乙种玩具需用金属100克，塑料120克.若工厂有金属4600克，塑料6440克，计划用两种材料生产甲、乙两种玩具共50件，求甲种玩具件数的取值范围.

1、(10分)我市一山区学校为部分家远的学生安排住宿，将部分教室改造成若干间住房. 如果每间住5人，那么有12人安排不下；如果每间住8人，那么有一间房还余一些床位，问该校可能有几间住房可以安排学生住宿？住宿的学生可能有多少人？

7.6一元一次不等式组(2) 同步练习

(总分：100分 时间45分钟)

13.3一次函数与一次方程、一次不等式同步练习

第1题. 函数y=kx+b，当时，y<0，则k与b的关系是(　)

A．2b>k B．2b<k C．2b>-k　　 D．2b<-k

第2题. 在函数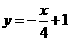中，若y的值不小于0．则x(　 )

A．x≤4 B．x≥4 C．x≤-4　　 D．x≥-4

第3题. 无论m为何实数，直线y=x+2m与y=－x+4的交点不可能在(　 )．

A．第一象限　　 B．第二象限

C．第三象限　　 D．第四象限

第4题. 若函数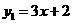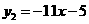，，且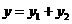，则y的值是13时，x的值是　　　 ．

第5题. 当x=2时，函数y=kx+10与y=3x+3k的值相等，则k的值是　　　 ．

第6题. 函数与函数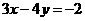的交点坐标为____．

第7题. 当x　　　 时，函数y=2x+3的值大于0．

第8题. 当x=2时，函数y=k x +10与y=3 x +3k的值相等，则k的值是______．

第9题.在同一直角坐标系中，有直线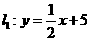和，请你求出当x在怎样的范围内直线l₁在直线l₂的上方．

第10题. 已知函数y=kx+b的图像经过(-1，-5)和(1，1)点．

(1)　　 当x取怎样的值时，y≥0；

(2)　 当x<2时，y值的范围是什么？

第11题. 已知函数y₁=3x+5，y₂=2x-1，当x　　　 时，有y₁＜y₂．

第12题. 当x=2时，函数y=kx+10与y=3x+3k的值相等，则k的值是　　　 .

第13题. 已知函数y₁=3x+5，,y₂=2x-1,当x　　　 时，有y₁＜y₂

第14题. 某校准备在甲、乙两家公司为毕业班学生制作一批纪念册．甲公司提出：每册收材料费5元，另收设计费1500元；乙公司提出：每册收材料费8元，不收设计费．

(1)请写出制作纪念册的册数与甲公司的收费(元)的函数关系式．

(2)请写出制作纪念册的册数与甲公司的收费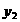(元)的函数关系式．

(3)如果学校派你去甲、乙两甲公司订做纪念册，你会选择哪家公司？

第15题.某化工厂生产某种化肥，每吨化肥的出厂价为1780元，其成本价为900元，但在生产过程中，平均每吨化肥有280立方米有害气体排出，为保护环境，工厂须对有害气体进行处理，现有下列两种处理方案可供选择：①将有害气体通过管道送交废气处理厂统一处理，则每立方米需付费3元；②若自行引进处理设备处理有害气体，则每处理1立方米有害气体需原料费0.5元，且设备每月管理、损耗等费用为28000元.设工厂每月生产化肥x吨，每月利润为y元(注：利润=总收入-总支出)

(1)分别求出用方案①、方案②处理有害气体时，y与x的函数关系式；

(2)根据工厂每月化肥产量x的值，通过计算分析工厂应如何选择处理方案才能获得最大利润.[

23、有一个附有进、出水管的容器，每单位时间内进、出的水量都是一定的，设从某时刻开始的4分钟内只有进水不出水，在随后的8分钟内既进水又出水，得到时间x(分)与水量y(升)之间的关系如图所示. (7分)

(1)每分钟进水多少？

(2)4≤x≤12时， 写出y与x的函数关系式.

(3)若12分钟后只放水不进水，在原来的坐标系中画出12分钟后的图象，并求y与x的函数关系式.

22、某公司在A、B两地分别有库存机器16台和12台，现要运往甲、乙两地，其中甲地15台，乙地13台.从A地运一台到甲地的运费为500元，到乙地为400元；从B地运一台到甲地的运费为300元，到乙地为600元.(1)设从A地调x台甲地,总运费为y元,写出y与x的函数关系式.并求出x的取值范围.(2)要使这些机器总运费最省,写出此时的调配方案？(7分)

21、如图表示甲乙两船沿相同路线从A港出发到B港行驶过程中路程随时间变化的图象，根据图象解答下列问题：(7分)

(1)请分别求出表示甲船和乙船行驶过程的函数解析式.

(2)问乙船出发多长时间赶上甲船？

20、如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象．(1)写出y与t之间的函数关系式．(2)通话2分钟应付通话费多少元？通话7分钟呢？(7分)

19、已知一次函数y=kx+b中自变量x的取值范围是-2≤x≤6，相应的函数取值范围是-11≤y≤9，求此函数解析式. (7分)

18、已知一条直线经过A(0，4)、点B(2，0)，如图.将这直线向左平移与x轴负半轴、y轴负半轴分别交于点C、点D，使DB=DC.求直线CD的函数解析式. (5分)