引导学生总结本节的主要知识点.

2.提示：先证△BDE≌△CDF(AAS).　 再由角平分线的性质定理及其逆定理即可得到结论.

1.提示：过点P分别向△ABC三边作垂线，由角平分线的性质定理及其逆定理即可证明结论.

2.在△ABC中，∠B=∠C，点D为BC边的中点，DE⊥AB， DF⊥AC，垂足分别是E，F.求证：点D在∠A的平分线上.

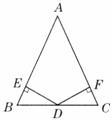
1.已知：如图，△ABC的角平分线BM，CN相交于点P.求证，点P到三条边AB，BC，CA的距离相等.

观察与思考

观察下面用尺规作角的平分线的步骤(如下图)，思考这种作法的依据.

步骤一：以点O为圆心，以适当长为半径画弧，弧与角的两边分别交于A，B两点.

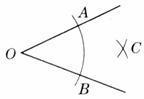
步骤二：分别以点A，B为圆心，以固定长(大于AB长的一半)为半径画弧，两弧交于点C

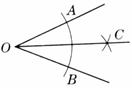
步骤三：作射线OC，则OC就是∠AOB的平分线.

注：独立完成用尺规作角平分线的过程，进一步培养学生的操作能力，并能说出作图过程中每步的依据.

依据是“SSS”公理和全等三角形的对应角相等.

3.写出证明过程.

注：类比“线段垂直平分线的性质定理及其逆定理”的学习过程，让学生独立完成“做一做”中提出的问题.

这样，我们就得到：

角平分线性质定理的逆定理　 到一个角的两边距离相等的点，在这个角的平分线上.

2.请根据逆命题的内容，画出图形，并结合图形，写出已知和求证.

做一做

1.请写出角平分线性质定理的逆命题.

我们已经探究出角平分线上的点所具有的性质，怎样对这个性质进行证明呢？

角平分线的性质定理 　角平分线上的点到这个角的两边的距离相等.

证明角平分线的性质定理时，我们将用到三角形全等判定公理的推论：

推论　 两角及其中一角的对边对应相等的两个三角形全等(AAS).

做一做

证明三角形全等判定公理的推论.

注：让学生独立按照证明的格式完成对“AAS”定理的证明，作为证明本节定理的依据.

证明略.

利用上面你已经证明的推论，可以对角平分线的性质定理给出如下的证明.

已知：如下图，OC是∠AOB的平分线，P是OC上任意一点，PD⊥OA，PE⊥OB，垂足分别为D，E.

求证：PD=PE.

证明：∴OC是∠AOB的平分线(已知)，

∴∠1=∠2(角平分线的定义).

∵PD⊥OA，PE⊥OB(已知)，

∴∠PDO=∠PEO=90°(垂直的定义).

在△PDO和△PEO中，

∠PDO=∠PEO (已证)，

∠1＝∠2(已证)，

OP＝OP(公共边)，

∴△PDO≌△PEO (AAS).

∴PD=PE(全等三角形的对应边相等).