8.四川模拟模拟 随着计算机技术的迅猛发展，电脑价格不断降低.某品牌电脑按原售价降低m元后，又降价20%，现售价为n元，那么该电脑的原售价为(　)

　A.(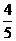n+m)元　B.(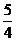n+m)元　C.(5m+n)元　D.(5n+m)元

　思路解析：列式表示原售价为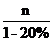+m.

　答案：B

7.(1)化简求值：(x-2)(x-3)+2(x+6)(x-5)-3(x²-7x+13)，其中x＝-.

　(2)已知|a-2|+(b-)²＝0，求-a(a²-2ab-b²)-b(ab+2a²-b²)的值.

　思路解析：先化简，后代值计算.两个非负数的和等于0时，这两个数同时为0.　解：(1)(x-2)(x-3)+2(x+6)(x-5)-3(x²-7x+13)

　＝x²-5x+6+2(x²+x-30)-3x²+21x-39

　＝x²-5x+6+2x²+2x-60-3x²+21x-39

　＝18x-93.

　当x＝-时，原式＝-100.

　(2)因为|a-2|+(b-)²＝0，

　所以a-2＝0，b-＝0，

　因此a＝2，b＝.

　-a(a²-2ab-b²)-b(ab+2a²-b²)＝-a³+2a²b+ab²-ab²-2a²b+b³＝-a³+b³.

　当a＝2，b＝时，原式＝-7.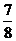

回顾·热身·展望

6.计算：

　(1)2(a⁵)²·(a²)²-(a²)⁴·(a²)²·a²；

　(2)(bⁿ)³·(b²)^m+3(b³)ⁿ·b²·(b^m-1)²；

　(3)(27×81×9²)².

　思路解析：综合运用运算性质进行运算，注意运算顺序与简便方法.

　答案：(1)原式=2a¹⁰·a⁴-a⁸·a⁴·a²=2a¹⁴-a¹⁴＝a¹⁴.

　(2)原式=b³ⁿ·b^2m+3b³ⁿ·b²·b^2m-2＝b³ⁿ+2m+3b³ⁿ+2m＝4b³ⁿ+2m.

　(3)(27×81×9²)²＝(3³×3⁴×3⁴)²＝(3¹¹)²＝3²².

5.如图15-2-2，AB＝a，P是线段AB上一点，分别以AP、BP为边作正方形.

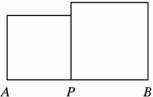
图15-2-2

　(1)设AP＝x，则两个正方形的面积之和S＝________；

　(2)当AP分别为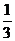a和a时，两个正方形的面积的和分别为S₁和S₂，比较S₁和S₂的大小：________.

　思路解析：(1)小正方形的面积＝x²，大正方形的面积＝(a-x)²，所以面积之和S＝x²+(a-x)²＝x²+(a-x)·(a-x)＝2x²-2ax+a².

　(2)当AP＝a时，代入得S＝a²；当AP＝a时，代入得S＝a²，所以S₁>S₂.

　答案：(1)2x²-2ax+a²　(2)S₁>S₂

综合·应用·创新

4.观察下列各式：1×3＝1²+2×1，2×4＝2²+2×2，3×5＝3²+2×3，…，请你将猜想到的规律用自然数n(n≥1)表示出来：________.

　思路解析：通过观察下列各式：1×3＝1²+2×1，2×4＝2²+2×2，3×5＝3²+2×3，…，可知“×”前是1，2，…，n等自然数，“×”后的自然数都比“×”前的大2，所以相应的是3，4，…，n+2，所以n(n+2)＝n²+2n.

　答案：n(n+2)＝n²+2n

3.-5·(-5)²=________；若x²ⁿ=4，则x⁶ⁿ=________；a¹²=(________)⁶=(________)³；若64⁴×8³＝2^x，则x=________.

　思路解析：灵活运用幂的运算性质.-5·(-5)²=-125；若x²ⁿ=4，则x⁶ⁿ=(x²ⁿ)³=4³=64；a¹²=(a²)⁶=(a⁴)³；若64⁴×8³=2^x，(2⁶)⁴×(2³)³=2²⁴×2⁹=2³³=2^x，则x=33.

　答案：-125　 64　 a²　 a⁴　 33

2.现规定一种运算：a*b＝ab+a-b，其中a、b为实数，则a*b+(b-a)*b等于(　)

　A.a²-b　B. b²-b　C.b²　D.b²-a

　思路解析：按规定的运算化简：a*b+(b-a)*b＝ab+a-b+ (b-a)b+(b-a)-b.

　答案：B[

1.下列各式中，计算过程正确的是(　)

　A.x³+x³＝x³⁺³＝x⁶

　B.x³·x³＝2x³＝x⁶

　C.x·x³·x⁵＝x⁰⁺³⁺⁵＝x⁸

　D.x²·(-x)³＝-x²⁺³＝-x⁵

　答案：D

24.8 角平分线的性质及其逆定理

第1题. 如图，△ABC中，AD为∠BAC的平分线，DE⊥AB，DF⊥AC，E、F为垂足，在以下结论中：①△ADE≌△ADF；②△BDE≌△CDF；③△ABD≌△ACD；④AE=AF；⑤BE=CF；⑥BD=CD．其中正确结论的个数是(　)

A．1　　 B．2　　 C．3　　 D．4

答案：B．

第2题. 如图，Rt△ABC中，∠C=90º，BD是角平分线，DE⊥AB，垂足为E，BC=6，CD=3，AE=4，则DE=_______，AD=_______，△ABC的周长是_______．

答案：3，5，24

第3题. 用三角尺画角平分线：如图，∠AOB是一个任意角，在边OA，OB上分别取OM=ON，再分别过M、N作OA，OB的垂线，交点为P，画射线OP，则这条射线即为角平分线．请解释这种做法的道理．你还能举出哪些作角平分线的方法，并说明这种做法的道理．

答案：提示：OM=ON，OP=OP，∴Rt△OMP≌Rt△ONP(HL)，∴∠MOP=∠NOP，∴射线OP是∠AOB的平分线．

第4题. 求证：三角形的三条角平分线相交于一点．

答案：提示：画出图形，写出已知、求证，证明两条角平分线的交点到第三个角的两边的距离相等．

第5题. 如图，三条公路围成的一个三角形区域，要在这个区域中建一个加油站，使它到三条公路的距离都相等，加油站应建在什么位置？请用尺规作图，找出建造加油站的位置．

答案：提示：作两个角的平分线，交点即为建加油站的位置．

第6题. 如图，△ABC中，∠C=90º，BD平分∠ABC交AC于D，DE是AB的垂直平分线，DE=BD，且DE=1.5cm，则AC等于(　)

A．3cm　 B．7.5cm　　 C．6cm　 D．4.5cm

答案：D．

第7题. 如图，△ABC中，P是角平分线AD，BE的交点．

求证：点P在∠C的平分线上．

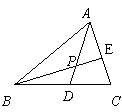
答案：如图，过点P作PM⊥AB，PN⊥BC，PQ⊥AC，垂足分别为M、N、Q．∵P在∠BAC的平分线AD上，∴PM=PQ．P在∠ABC的平分线BE上，∴PM=PN。∴PQ=PN，∴点P在∠C的平分线．

第8题. 如图，已知点D是∠ABC的平分线上一点，点P在BD上，PA⊥AB，PC⊥BC，垂足分别为A，C．

求证：(1)AD=CD；(2)∠ADB=∠CDB．

答案：△ABP≌△CBP，∴AB=CB，又∠ABP=∠CBP，BD=BD，∴△ABD≌△CBD，∴AD=CD，∠ADB=∠CDB．

第9题. 如图，在∠AOB的两边OA，OB上分别取OM=ON，OD=OE，DN和EM相交于点C．

求证：点C在∠AOB的平分线上．

答案：提示：作CE⊥OA于E，CF⊥OB于F，OM=ON，OE=OD，∠MOE=∠NOD，∴△MOE≌△NOD(SAS)，∴S_{△M O E} =S_{△N O D}，同时去掉S_{四边形ODCE}，得S_{△M D C}=S_{△N E C}，易证，MD=NE，∴CE=CF，∴点C在∠AOB的平分线上．

第10题. 已知：如图，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，E、F分别为垂足．

求证：AD垂直平分EF．

答案：提示：由角平分线的性质定理，可得DE=DF，进而求得∠DEF=∠DFE，∠AEF=∠AFE，所以AE=AF，所以AD垂直平分EF．

第11题. 如图，已知△ABC中，∠C=90º，∠BAC=2∠B，D是BC上一点，DE⊥AB于E，DE=DC．

求证：AD=BD．

答案：提示：DE=DC，AD=AD，∴Rt△ADE≌Rt△ADC，∴∠EAD=∠DAC=∠BAC，又∠B=∠BAC，∴∠EAD=∠B，∴AD=BD．