26.1平均数与加权平均数

1，先画出一个10×10的正方形网格，再根据要求，在画出的方格图中画出图形：　　　

⑴画出四边形ABCD关于点D成中心对称的图形A′B′C′D′，

⑵将图形A′B′C′D′向右平移3格，再向下平移2格后的图形A″B″C″D″．

2，四边形ABCD是正方形，△ADF旋转一定角度后得到△ABE，如图7所示，如果AF＝4，AB＝7，求(1)指出旋转中心和旋转角度(2)求DE的长度(3)BE与DF的位置关系如何？

3，在△ABC中，∠B＝10°，∠ACB＝20°，AB＝4cm，△ABC逆时针旋转一定角度后与△ADE重合，且点C恰好成为AD中点，如图8，⑴指出旋转中心，并求出旋转的度数。⑵求出∠BAE的度数和AE的长．

4，如图9所示，平移正方形网格中的阴影图案，使点A移到A₁的位置，然后再向下平移两格．

5，平移如图10所示方格纸中的图形，使点A平移到A₁，画出平移后的图形．

6，如图11，两个村庄A和B被一条河隔开，现要在河上架设一座桥CD，请你为两村设计桥址，使由A村到B村的距离最小(假定两河岸m，n是平行的，且桥要与河垂直)，要求还要写出作法，并说明理由．

7，如图12所示，ΔABC中，AB＝AC，AC+BC＝14cm，沿着CB的方向把AB边平移BC，连结AD和BE，那么四边形ACED是什么图形？请求出它的周长．

8，将RtΔABC沿直角边AB向右平移2个单位得到RtΔDEF，如图13所示，若AB＝4，∠ABC＝90°，且△ABC的面积为6个平方单位，试求图中阴影部分的面积．

9，如图14，在正方形ABCD中，G是BC上的一点，连结AG，作AG的垂线EF交AB于E点，交CD于F点，已知AG＝10cm，求EF的长．

8，如图9，把三角形△ABC绕着点C顺时针旋转35°，得到△A′B′C，A′B′交AC于点D，若∠A′DC＝90°，则∠A的度数是＿＿＿．

9，如图10，AD是△ABC的高线，且AD＝2，若将△ABC及其高线平移到△A′B′C′的位置，则A′D′和B′D′位置关系是＿＿＿，A′D′＝＿＿＿．

10，如图11，△ABC绕点B逆时针方向旋转到△EBD的位置，若∠A＝15°，∠C＝10°，E，B，C在同一直线上，则∠ABC＝＿＿＿，旋转角度是＿＿＿．

1，如果△ABC经过平移后得到△DEF，若∠A＝41°，∠C＝32°，EF＝3cm，则∠E＝＿＿，BC＝＿＿cm．

2，如果△ABC沿着北偏东35°的方向移动了6cm，那么△ABC的一条角平分线AD上的中点Q向＿＿＿＿＿＿＿方向移动了＿＿＿＿cm．

3，将一图形沿着正北方向平移5cm后，再沿着正西方向平移5cm，这时图形在原来位置的＿＿＿＿方向上．

4，如图4，已知梯形ABCD，AD∥BC，BC＝6，AD＝3，AB＝4，CD＝2，AB平移后到DE处，则ΔCDE的周长是＿＿＿．

5，如图5，△ABC以点A为旋转中心，按逆时针方向旋转60°，得△AB＇C＇，则△ABB＇是＿＿＿三角形．

6，如图6，在四边形ABCD中，AD∥BC，BC＞AD，∠B与∠C互余，将AB，CD分别平移到EF和EG的位置，则△EFG为＿＿＿三角形，若AD＝2cm，BC＝8cm，则FG＝＿＿＿．

1，下列运动属于平移的是(　　)

A．空中放飞的风筝

B．飞机在跑道上滑行到停止的运动　

C．球运动员投出并进入篮筐的过程　

D．乒乓球比赛中的高抛发球后，乒乓球的运动方式

2，下列说法正确的是(　 )

A．平移不改变图形的形状和大小，而旋转则改变图形的形状和大小

B．平移和旋转的共同点是改变图形的位置

C．图形可以向某方向平移一定距离，也可以向某方向旋转一定距离

D．在平移和旋转图形中，对应角相等，对应线段相等且平行

3，如图1，△DEF是由△ABC经过平移后得到的，则平移的距离是(　 )

A．线段BE的长度　　　　　　 B．线段EC的长度

C．线段BC的长度　　　　　　 D．线段EF的长度

4，将一图形绕着点O顺时针方向旋转70°后，再绕着点O逆时针方向旋转120°，这时如果要使图形回到原来的位置，需要将图形绕着点O什么方向旋转的度是(　　 )

A．顺时针方向50°　 B．逆时针方向50°　C．顺时针方向190°　 D．逆时针方向190°

5，如图2，图形旋转一定角度后能与自身重合,则旋转的角度可能是(　　 )　　　　

A．30°　　　 B．60°　 　　 C．90°　 　　 D．120°

6，如图3，面积为12cm²的△ABC沿BC方向平移至△DEF的位置，平移的距离是边BC长的两倍，则图中的四边形ACED的面积为(　　 )

A．24cm²　　 B．36cm²　　 C．48cm²　　　 D．无法确定

24.3 平行线的判定定理

第1题. 如图，直线a、b都与直线c相交，下列条件中，能判断a∥b的条件是(　)

①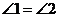②③④

A．①③ B．①②④　 C．①③④　 D．②③④

答案：B．

第2题. 如图，DE是过点A的直线，要使DE∥BC，应有(　)

A． B．

C． D．

答案：C．

第3题. 看图填理由：

∵直线AB，CD相交于O，(已知)

∴∠1与∠2是对顶角

∴∠1=∠2(___________________)

∵∠3+∠4=180°(已知)

∠1+∠4=180°(__________________)

∴∠1=∠3(__________________)

∴CD//AB(__________________)

答案：对顶角相等；平角定义；同角的补角相等；同位角相等，两直线平行．

第4题. 如图：AB∥CD，．

答案：．

24.4 平行线的性质定理

第1题. 命题“线段垂直平分线上的点到这条线段两个端点的距离相等”．的逆命题是

_________________________________________________．

答案：如果一个点到线段两个端点的距离相等，那么这个点在这条线段的垂直平分线上．

第2题. 下列命题中的逆命题正确的是(　)

A．如果a=b，则a²=b²

B．对顶角相等

C．若三角形中有一个角是钝角，则其余两个角都是锐角

D．线段垂直平分线上的点到这条线段的两个端点距离相等

答案：D．

第3题. 下列说法正确的是(　)

A．在同一平面内两条直线被第三条直线所截，同旁内角互补

B．如果一个角的两边分别平行于另一个角的两边，那么这两个角一定相等

C．两个相等的角一组边平行，那么另一组边也平行

D．一条直线垂直于平行线中的一条，也一定垂直于另一条

答案：D．

甲、乙两同学做“投球进筐”游戏．商定：每人玩5局，每局在指定线外将一个皮球投往筐中，一次未进可再投第二次，以此类推，但最多只能投6次，当投进后，该局结束，并记下投球次数；当6次都未投进时，该局也结束，并记为“×”．两人五局投球情况如下：

(1)为了计算得分，双方约定：记“×”为该局得0分，其他局得分的计算方法要满足两个条件：①投球次数越多，得分越低；②得分为正数．请你按约定的要求，用公式、表格、语言叙述等方法，选取其中一种写出一个将其他局的投球次数换算成得分的具体方案；

(2)请根据上述约定和你写出的方案，计算甲、乙两人的各局得分，填入牌上的表格中，并从平均分的角度来判断谁投得最好．

5．(本题12分)某国家的一工厂职工的月工资及人数如下表：

(1)求月工资的平均数，工厂主用这个平均数作为代表数，这是为什么?

(2)求月工资的众数，工会领导用众数作为代表数，这是为什么？

(3)求月工资的中位数，税务员用中位数作为代表数，这是为什么？

4．(本题12分)八(3)班的小明、小刚、小强正为谁的数学成绩最好而争论，他们三人的五次数学成绩如表1所示，这五次数学成绩的平均数、中位数、众数如表2所示：

表1：

表2：

现在这三位同学都说自己的数学成绩是最好的．

(1)请你猜猜他们各自的理由;

(2)三人似乎都有道理，你对此有何看法？请运用统计知识作出正确的分析．

3．(本题12分)若某校对各个班级的教室卫生检查成绩如下表所示：

(1)若按平均成绩计算，哪班卫生成绩最好？

(2)若将地面、门窗、桌椅、黑板按40%，35%，15%，10%的比例计算各班卫生成绩，那么哪个班的成绩最高？

(3)试统计你校八年级各个班地面、门窗、桌椅、黑板的卫生成绩，并分别按(1)、(2)的评分标准计算成绩，看看你所在班级的卫生情况，你将怎样继续改进?