3. 若正方形的4个顶点分别在直角三角形的3条边上，直角三角形的两直角边的长分别为3cm和4cm，则此正方形的边长为____________。

(2000年武汉市中考题)

2. 如图，△ABC中，CE：EB＝1：2，DE∥AC，若△ABC的面积为S，则△ADE的面积为____________。

1. 如图，已知DE∥BC，CD和BE相交于O，若，则AD：DB＝____________。

3. 相似三角形的识别

　　 (1)如果一个三角形的两角分别与另一个三角形的两角对应相等，那么这两个三角形相似。

　　 (2)如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似。

　　 (3)如果一个三角形的三条边和另一个三角形的三条边对应成比例，那么这两个三角形相似。

[典型例题]

　 例1. 如图，∠1＝∠2＝∠3，图中相似三角形有(　　 )对。

　　 答：4对

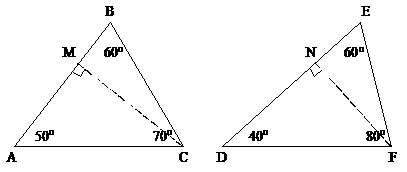
　 例2. 如图，已知：△ABC、△DEF，其中∠A＝50°，∠B＝60°，∠C＝70°，∠D＝40°，∠E＝60°，∠F＝80°，能否分别将两个三角形分割成两个小三角形，使△ABC所分成的每个三角形与△DEF所分成的每个三角形分别对应相似？

　　 如果可能，请设计一种分割方案；若不能，说明理由。

　 　解：

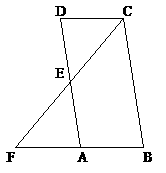
　 例3. (2004·广东省)如图所示，四边形ABCD是平行四边形，点F在BA的延长线上，连结CF交AD于点E。

　　 (1)求证：△CDE∽△FAE；

　　 (2)当E是AD的中点，且BC＝2CD时，求证：∠F＝∠BCF。

　　 命题意图：相似三角形的识别、特征在解题中的应用。

　　 解析：由AB∥DC得：∠F＝∠DCE，∠EAF＝∠D

　　 ∴△CDE∽△FAE

　　 ，又E为AD中点

　　 ∴DE＝AE，从而CD＝FA，结合已知条件，易证

　　 BF＝BC，∠F＝∠BCF

　　 解：(1)∵四边形ABCD是平行四边形

　　 ∴AB∥CD

　　 ∴∠F＝∠DCE，∠EAF＝∠D

　　 ∴△CDE∽△FAE

　　 (2)∵E是AD中点，∴DE＝AE

　　 由(1)得：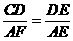

　　 ∴CD＝AF

　　 ∵四边形ABCD是平行四边形

　　 ∴AB＝CD

　　 ∴AB＝CD＝AF

　　 ∴BF＝2CD，又BC＝2CD

　　 ∴BC＝BF

　　 ∴∠F＝∠BCF

　 　思路探究：平行往往是证两个三角形相似的重要条件，利用比例线段也可证明两线段相等。

　 例4. 在梯形ABCD中，∠A＝90°，AD∥BC，点P在线段AB上从A向B运动，

　　 (1)是否存在一个时刻使△ADP∽△BCP；

　　 (2)若AD＝4，BC＝6，AB＝10，使△ADP∽△BCP，则AP的长度为多少？

　 　解：(1)存在

　　 (2)若△ADP∽△BCP，则

　　 设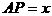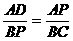

　　 或

　　 或

　　 或

　　 ∴AP长度为4或6

　 例5. 如图，在平行四边形ABCD中，E为CD上一点，DE：CE＝2：3，连结AE、BE、BD，且AE、BD交于点F，则(　　 )

　　 A. 4：10：25　　　　　　 B. 4：9：25

　　 C. 2：3：5　　　　　　　 D. 2：5：25

(2001年黑龙江省中考题)

　 　思路点拨：运用与面积相关知识，把面积比转化为线段比。

　　 ∴选A

　 例6. 如图，有一批形状大小相同的不锈钢片，呈直角三角形，已知∠C＝90°，AB＝5cm，BC＝3cm，试设计一种方案，用这批不锈钢片裁出面积达最大的正方形不锈钢片，并求出这种正方形不锈钢片的边长。

　 　思路点拨：要在三角形内裁出面积最大的正方形，那么这正方形所有顶点应落在△ABC的边上，先画出不同方案，把每种方案中的正方形边长求出。

　　 解：如图甲，设正方形EFGH边长为x，则AC＝4

　　 而CD×AB＝AC×BC＝，得

　　 又△CEH∽△CAB，得

　　 于是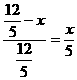，解得：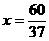

　　 如图乙，设正方形CFGH的边长为y cm

　　 由GH∥AC，得：

　　 即，解得：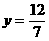

　　 即应如图乙那样裁剪，这时正方形面积达最大，它的边长为

　 例7. 如图，已知直角梯形ABCD中，∠A＝∠B＝90°，设，，作DE⊥DC，DE交AB于点E，连结EC。

　　 (1)试判断△DCE与△ADE、△DCE与△BCE是否分别一定相似？若相似，请加以证明。

　　 (2)如果不一定相似，请指出a、b满足什么关系时，它们就能相似？

　　 解：(1)△DCE与△ADE一定相似，△DCE与△BCE不一定相似，分别延长BA、CD交于F点

　　 由△FAD∽△FBC，得：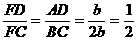

　　 于是FD＝DC，从而可证△FED≌△CED

　　 得∠AED＝∠DEC

　　 所以△DEC∽△AED

　　 (2)作CG⊥AD交AD延长线于G，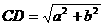

　　 由△AED∽△GDC，有，得

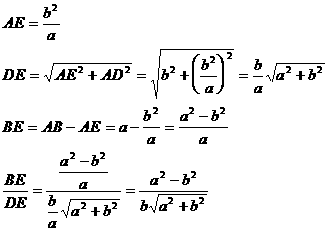
　　 要使△DCE与△BCE相似，那么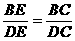一定成立

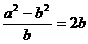　　 即，得

　　 也就是当时，△DCE与△BCE一定相似。

[模拟试题](答题时间：40分钟)

2. 相似比

　　 相似三角形对应边的比叫做相似比。

　　 说明：相似比要注意顺序：如△ABC∽△A'B'C'的相似比，而△A'B'C'∽△ABC的相似比，这时。

1. 相似三角形

　　 对应角相等，对应边成比例的三角形叫做相似三角形(similar triangles)。

　　 议一议：

　　 (1)两个全等三角形一定相似吗？为什么？

　　 (2)两个直角三角形一定相似吗？两个等腰直角三角形呢？为什么？

　　 (3)两个等腰三角形一定相似吗？两个等边三角形呢？为什么？

2. 通过相似三角形性质复习，丰富与角、面积等相关的知识方法，开阔研究角、面积等问题的视野。

[知识纵横]

1. 通过探索两个三角形相似的识别方法，加强合情推理能力的培养，感受发现的乐趣，逐步掌握说理的基本方法。

4.2 相似三角形 同步练习

重点、难点：