
题目列表(包括答案和解析)
8. 若关于x的方程x2+2(k-1)x+k2=0有实数根,则k的取值范围是
A.  B.
B.
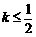 C.
C.  D.
k≥
D.
k≥
7. 已知正比例函数y=k1x(k1≠0)与反比例函数y= (k2≠0)的图象有一个交点的坐标为(-2,-1),则它的另一个交点的坐标是
(k2≠0)的图象有一个交点的坐标为(-2,-1),则它的另一个交点的坐标是
A. (2,1) B. (-2,-1) C. (-2,1) D. (2,-1)
6. 如图2,若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点,为使△ABC∽△PQR,则点R应是甲、乙、丙、丁四点中的
如图2,若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点,为使△ABC∽△PQR,则点R应是甲、乙、丙、丁四点中的
A. 甲 B. 乙
C. 丙 D. 丁
5. 若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则 的值为
的值为
A.  B.
99! C.
9900 D. 2!
B.
99! C.
9900 D. 2!
4. 下列命题中,正确的是
A. 同位角相等 B. 平行四边形的对角线互相垂直平分
C. 等腰梯形的对角线互相垂直 D. 矩形的对角线互相平分且相等
3. 某服装销售商在进行市场占有率的调查时,他最应该关注的是
A. 服装型号的平均数 B. 服装型号的众数
C. 服装型号的中位数 D. 最小的服装型号
2. 图1所示的几何体的右视图是

1.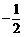 的绝对值是
的绝对值是
A. -2 B.
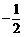 C.
2 D.
C.
2 D. 
28、(7分)随着海峡两岸交流日益增强,通过“零关税”进入我市的一种台湾水果,其进货成本是每吨0.5万元,这种水果市场上的销售量 (吨)是每吨的销售价
(吨)是每吨的销售价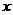 (万元)的一次函数,且
(万元)的一次函数,且 时,
时, ;
; 时,
时, 。
。
(1)求出销售量 (吨)与每吨的销售价
(吨)与每吨的销售价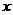 (万元)之间的函数关系式;
(万元)之间的函数关系式;
(2)若销售利润为 (万元),请写出
(万元),请写出 与
与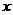 之间的函数关系式,并求出销售价为每吨2万元时的销售利润。
之间的函数关系式,并求出销售价为每吨2万元时的销售利润。
29﹡、(8分)为了解决农民工子女入学难的问题,我市建立了一套进城农民工子女就学的保障机制,其中一项就是免交“借读费”。据统计,2004年秋季有5000名农民工子女进入主城区中小学学习,预测2005年秋季进入主城区中小学学习的农民工子女将比2004年有所增加,其中小学增加20%,中学增加30%,这样,2005年秋季将新增1160名农民工子女在主城区中小学学习。
(1)如果按小学每生每年收“借读费”500元,中学每生每年收“借读费”1000元计算,求2005年新增的1160名中小学生共免收多少“借读费”?
(2)如果小学每40名学生配备2名教师,中学每40名学生配备3名教师,若按2005年秋季入学后,农民工子女在主城区中小学就读的学生人数计算,一共需要配备多少名中小学教师?
30﹡、(8分)如图,AB是△ABC的外接圆⊙O的直径,D是⊙O上的一点,DE⊥AB于点E,且DE的延长线分别交AC、⊙O、BC的延长线于F、M、G。
(1)求证:AE·BE=EF·EG;
(2)连结BD,若BD⊥BC,且EF=MF=2,求AE和MG的长。

31﹡、(10分)已知抛物线 与
与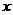 轴交于A、B两点,且点A在
轴交于A、B两点,且点A在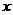 轴的负半轴上,点B在
轴的负半轴上,点B在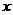 轴的正半轴上。
轴的正半轴上。
(1)求实数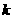 的取值范围;
的取值范围;
(2)设OA、OB的长分别为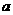 、
、 ,且
,且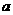 ∶
∶ =1∶5,求抛物线的解析式;
=1∶5,求抛物线的解析式;
(3)在(2)的条件下,以AB为直径的⊙D与 轴的正半轴交于P点,过P点作⊙D的切线交
轴的正半轴交于P点,过P点作⊙D的切线交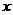 轴于E点,求点E的坐标。
轴于E点,求点E的坐标。
32﹡、(10分)已知四边形ABCD中,P是对角线BD上的一点,过P作MN∥AD,EF∥CD,分别交AB、CD、AD、BC于点M、N、E、F,设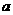 =PM·PE,
=PM·PE, =PN·PF,解答下列问题:
=PN·PF,解答下列问题:
(1)当四边形ABCD是矩形时,见图1,请判断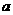 与
与 的大小关系,并说明理由;
的大小关系,并说明理由;
(2)当四边形ABCD是平行四边形,且∠A为锐角时,见图2,(1)中的结论是否成立?并说明理由;
(3)在(2)的条件下,设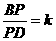 ,是否存在这样的实数
,是否存在这样的实数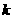 ,使得
,使得 ?若存在,请求出满足条件的所有
?若存在,请求出满足条件的所有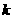 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。

重庆市2005年初中毕业暨高中招生统一考试
27、(8分)据2005年5月10日《重庆晨报》报道:我市四月份空气质量优良,高居全国榜首,某校初三年级课外兴趣小组据此提出了“今年究竟能有多少天空气质量达到优良”的问题,他们根据国家环保总局所公布的空气质量级别表(见表1)以及市环保监测站提供的资料,从中随机抽查了今年1-4月份中30天空气综合污染指数,统计数据如下:
表1:空气质量级别表
|
空气污染指数 |
0-50 |
51-100 |
101-150 |
151-200 |
201-250 |
251-300 |
大于300 |
|
空气质量级别 |
Ⅰ级(优) |
Ⅱ级(良) |
Ⅲ级1(轻微污染) |
Ⅲ级2(轻度污染) |
Ⅳ1(中度污染) |
Ⅳ2(中度重污染) |
Ⅴ(重度污染) |
空气综合污染指数
30,32,40,42,45,45,77,83,85,87,90,113,127,153,167
38,45,48,53,57,64,66,77,92,98,130,184,201,235,243
请根据空气质量级别表和抽查的空气综合污染指数,解答以下问题:
(1)填写频率分布表中未完成的空格:
|
分组 |
频数统计 |
频数 |
频率 |
|
0-50 |
 |
|
0.30 |
|
51-100 |
 |
12 |
0.40 |
|
101-150 |
|
|
|
|
151-200 |
 |
3 |
0.10 |
|
201-250 |
 |
3 |
0.10 |
|
合计 |
30 |
30 |
1.00 |
(2)写出统计数据中的中位数、众数;
(3)请根据抽样数据,估计我市今年(按360天计算)空气质量是优良(包括Ⅰ、Ⅱ级的天数)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com