
题目列表(包括答案和解析)
4.如图,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOB+∠DOC的值
 A 小于180°或等于180° B 等于180°
A 小于180°或等于180° B 等于180°
C 大于180° D 大于180°或等于180°
3.两位同学在描述同一反比例函数的图像时,甲同学说:这个反比例函数图像上任意一点到两坐标轴的距离的积都是3;乙同学说:这个反比例函数的图像与直线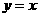 有两个交点,你认为这两位同学所描述的反比例函数的解析式是
( )
有两个交点,你认为这两位同学所描述的反比例函数的解析式是
( )
A 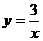 B
B 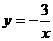 C
C  D
D 
2.已知关于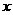 的不等式组
的不等式组 ,无解,则
,无解,则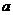 的取值范围是
( )
的取值范围是
( )
A 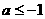 B
B 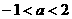 C
C 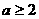 D
D 
1.下列式子的结果为负数的是 ( )
A  B
B 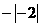 C
C  D
D
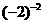
24. (本小题满分9分)
(本小题满分9分)
如图9,已知O为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).
(1) 求点B的坐标;
(2) 若二次函数y=ax2+bx+c的图象经过A、B、O三点,求此二次函数的解析式;
(3) 在(2)中的二次函数图象的OB段(不包括点O、B)上,是否存在一点C,使得四边形ABCO的面积最大?若存在,求出这个最大值及此时点C的坐标;若不存在,请说明理由.

资阳市2005年初中课改毕业年级学业考试暨高中阶段学校招生考试
22. (本小题满分8分)
(本小题满分8分)
 甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图7. 根据图象解决下列问题:
甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图7. 根据图象解决下列问题:
(1) 谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
(2) 分别求出甲、乙两人的行驶速度;
(3) 在什么时间段内,两人均行驶在途中(不包括起点和终点)?在这一时间段内,请你根据下列情形,分别列出关于行驶时间x的方程或不等式(不化简,也不求解):① 甲在乙的前面;② 甲与乙相遇;③ 甲在乙后面.
21. (本小题满分8分)
(本小题满分8分)
已知某项工程由甲、乙两队合做12天可以完成,共需工程费用13800元,乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的2倍少10天,且甲队每天的工程费用比乙队多150元.
(1) 甲、乙两队单独完成这项工程分别需要多少天?
(2) 若工程管理部门决定从这两个队中选一个队单独完成此项工程,从节约资金的角度考虑,应该选择哪个工程队?请说明理由.
20. (本小题满分7分)
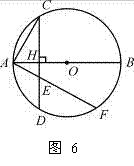 如图6,已知AB为⊙O的直径,弦CD⊥AB,垂足为H.
如图6,已知AB为⊙O的直径,弦CD⊥AB,垂足为H.
(1) 求证:AH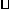 AB=AC2;
AB=AC2;
(2) 若过A的直线与弦CD(不含端点)相交于点E,与⊙O相交于点F,求证:AE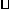 AF=AC2;
AF=AC2;
(3) 若过A的直线与直线CD相交于点P,与⊙O相交于点Q,判断AP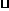 AQ=AC2是否成立(不必证明).
AQ=AC2是否成立(不必证明).
19. (本小题满分7分)
(本小题满分7分)
甲、乙两同学开展“投球进筐”比赛,双方约定:① 比赛分6局进行,每局在指定区域内将球投向筐中,只要投进一次后该局便结束;② 若一次未进可再投第二次,以此类推,但每局最多只能投8次,若8次投球都未进,该局也结束;③ 计分规则如下:a. 得分为正数或0;b. 若8次都未投进,该局得分为0;c. 投球次数越多,得分越低;d. 6局比赛的总得分高者获胜 .
(1) 设某局比赛第n(n=1,2,3,4,5,6,7,8)次将球投进,请你按上述约定,用公式、表格或语言叙述等方式,为甲、乙两位同学制定一个把n换算为得分M的计分方案;
(2) 若两人6局比赛的投球情况如下(其中的数字表示该局比赛进球时的投球次数,“×”表示该局比赛8次投球都未进):
|
|
第一局 |
第二局 |
第三局 |
第四局 |
第五局 |
第六局 |
|
甲 |
5 |
× |
4 |
8 |
1 |
3 |
|
乙 |
8 |
2 |
4 |
2 |
6 |
× |
根据上述计分规则和你制定的计分方案,确定两人谁在这次比赛中获胜.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com