8.　　　 正比例函数直线过原点y=kx(k是常数，k≠0)。

7.　　　 一次函数一条直线y=kx+b(k,b是常数，k≠0)。

6.　　　 函数的表示方法：解析法、图像法、列表法。

5.　　　 函数：设在一个变化过程中有两个变量x、y，对于x 的每一个值，y都有唯一的值与它相对应，则y叫做x的函数。其中x是自变量。

4.　　　 对称的点的坐标特征：

①　　 点P(a,b)关于x轴的对称点的坐标P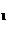(a,-b)。即：点P、P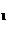关于x轴对称横坐标相同、纵坐标互为相反数。

②　　 点P(a,b)关于y轴的对称点的坐标P(-a,b)。即：点P、P关于x轴对称纵坐标相同、横坐标互为相反数。

③　　 点P(a,b)关于原点对称的点的坐标P(-a,-b)。即：点P、P关于原点对称横、纵坐标均互为相反数。

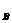3.　　　 设平面上点A(x,y),点B(x,y)：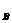

①　　 AB在x轴上或平行于x轴AB=｜x- x｜。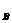

②　　 AB在y轴上或平行于y轴AB=｜y- y｜。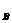

③　　 点A到原点的距离OA=。

④　　 平面上任意两点AB的距离AB=。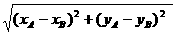

2.　　　 每一象限内点的坐标特征：设A(x,y)有

①　　 第一象限内的点x＞0,y＞0.

②　　 第二象限内的点x＜0,y＞0.

③　　 第三象限内的点x＜0, y＜0.

④　　 第四象限内的点x＞0, y＜0.

2．特殊位置的点的坐标特征：

①　　 横坐标上的点纵坐标为零。

②　　 纵坐标上的点横坐标为零。

③　　 平行于x轴的直线上的点纵坐标相等。

④　　 平行于y轴的直线上的点横坐标相等。

⑤　　 第一、三象限角平分线上的点横、纵坐标相等[设A点的坐标为(x,y)有x=y].

⑥　　 第二、四象限角平分线上的点横、纵坐标互为相反数[设A点的坐标为(x,y)有x= - y].

1.　　　 一一对应：

①　　 数轴上的点与实数一一对应。

②　　 坐标平面上的与有序实数对一一对应。