22、(本题10分)某企业有员工300人，生产A种产品，平均每人每年可创造利润m万元(m为大于零的常数)。为减员增效，决定从中调配x人去生产新开发的B种产品。根据评估，调配后，继续生产A种产品的员工平均每人每年创造的利润可增加20%，生产B种产品的员工平均每人每年可创造利润1.54m万元。

(1)调配后，企业生产A种产品的年利润为　　　　 　万元，企业生产B种产品的年利润为　　　　　 　万元(用含x和m的代数式表示)。若设调配后企业全年总利润为y万元，则y关于x的函数解析式为　　　　　　　　　 　。

(2)若要求调配后，企业生产A种产品的年利润不小于调配前企业年利润的，生产B种产品的年利润大于调配前企业年利润的，应有哪几种调配方案？请设计出来，并指出其中哪种方案全年总利润最大(必要时，运算过程可保留3个有效数字)。

(3)企业决定将“(2)”中的年最大总利润(设m=2)继续投资开发新产品。现有6种产品可供选择(不得重复投资同一种产品)，各产品所需资金及所获利润如下表：

　　　 如果你是企业决策者，为使此项投资所获年利润不少于145万元，你可以投资开发哪些产品？请写出两种投资方案。(不写解题过程)

21、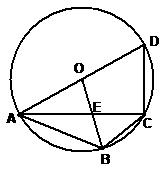如图，四边形ABCD内接于⊙O，已知直径AD=2，

∠ABC=120°，∠ACB=45°，连OB交AC于点E。

(1)　　 求AC的长；

(2)　　 求CE︰AE的值；

(3)　　 在CB的延长线上取一点P，使PB=2BC，试判断

直线PA和⊙O的位置关系，并证明你的结论。

20、解方程组：

19、计算：

18、一堆有红、白两种颜色的球各若干个，已知白球的个数比红球少，但白球个数的2倍比红球多。若把每一个白球都记作“2”，每一个红球都记作“3”，则总数为60，则白球最多有　　　　 个

17、从甲、乙、丙三人中选取2人去参加运动会有甲和乙、甲和丙、乙和丙3种不同的选法。抽象成数学模型即：从3个元素中选取2个元素的组合，记作 ；一般地，从m个元素中选取n个元素(n≤m)的组合，记作。根据以上分析从8人中选取5人去参加运动会的不同选法有　　　　　　 种。

16、如图，矩形ABCD中，AB=12，AD=10，将此矩形折叠，

使点B落在AD边的中点处，则折痕FG的长为　　　　

15、关于x的一元二次方程(k-1)x²-2x+3=0有两个不相等的实数根，则k的取值范围是　　　　　　　　

14、不等式组 的正整数解是　 　　　　　　　　

13、因式分解：a²-4b²+4b-1=