
题目列表(包括答案和解析)
4、已知,AB是⊙O的直径,BC是⊙O的弦,⊙O的割线PDE垂直于AB于点F,交BC于点G,∠A=∠BCP.
(1) 求证:PC是⊙O的切线;
(2) 若点C在劣弧AD上运动,其条件不变,问应再具备什么条件可使结论BG2=BF·BO成立,(要求画出示意图并说明理由).

3、如图,CD是⊙O的直径,E为⊙O中半圆一动点,过E点的⊙O的切线交CD的延长线于点A,过C点的⊙O的切线交AB于点B,直线OB交⊙O于点F、G。
①求证:DE∥BG;②若AE=4,AD=2,求tg∠AED的值;
③若GD的延长线与AB垂直,且⊙O的半径为3,求四边形BEDG的面积。

2、已知:C是⊙O的直径AB上一点,PC⊥AB与⊙O相交于E,PD是⊙O的切线,D是切点
求证:PC2=PD2+ACŸCB
选择题
1、直线和圆相交,圆的半径为R,直线到圆心的距离为5,则( )
(A) R>5 (B) R<5 (C) R=5 (D) R≥5
2、下列判断正确的是( )
(A) 经过圆心且垂直于切线的直线必经过切点
(B) 过半径外端的直线和圆相切
(C) 和圆只有一个公共点的线段叫圆的切线
(D) 垂直于圆的半径的直线和圆相切
3、若四边形ABCD是圆的外切四边形,则下列各式中正确的是( )
(A) AB+BC=AD+DC (B) AB+CD=BC+DA

(C) ∠A+∠B=180° (D) ∠A+∠C=180°
4、如图(1):弧ACB是一个半圆,CD⊥AB于点D,若AD=4,BD=2,则CD的长是( )
(A) 2 (B)2

(C) (D)4
5、如图(2):PA、PB、DE分别切⊙O于A、B、C,
如果⊙O的半径是6cm,PO长为10cm,
那么△PDE的周长是 ( )cm
(A) 16cm (B)14cm
(C) 12cm (D)10cm
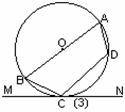
6、如图(3):四边形ABCD为圆内接四边形,AB为直径,MN切⊙O于C点,∠BCM=38°则∠ABC=( )
(A) 38° (B) 52°
(C) 68° (D) 42°
7、如图(4):过等腰△ABC的顶点A作这个三角形外接圆的切线AE,则∠DAE与∠ABC的大小关系为 ( )

(A) ∠DAE>∠ACB (B) ∠DAE=∠ACB
(C) ∠DAE<∠ACB (D) 无法确定
8、若PT是⊙O的切线,T是切点,PAB是割线,交⊙O于A、B,且过O点,若∠OPT=30°,PT=10cm,则PB长为( )
(A) cm (B) cm
(C) cm (D) 10cm
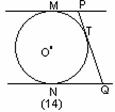
9、如图(14),MP和NQ是半径为r的圆的两条平行切线,M、N是切点,PTQ是第三条切线,T是切点,若MP=4,NQ=9,则r=( )
(A) 12 (B) 6
(C) (D) 无法确定
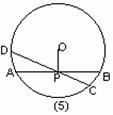
10、如图(5),⊙O的半径为6cm,弦心距OP为4cm,AB分弦CD为2∶3,则弦CD的长为( )cm
(A) 8 (B)
(C) (D)
解答题

1、如图,已知:DP为⊙O的直径,以P为圆心作一个圆,⊙O的弦BA所在直线与⊙P切于点C
求证:PAŸPB=PCŸPD

7、如图,抛物线 与
与 轴交点为A 、B(A在B左侧),与
轴交点为A 、B(A在B左侧),与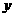 轴交点为C ,顶点为P,连结PC并延长交
轴交点为C ,顶点为P,连结PC并延长交 轴于点N。
轴于点N。
(1) 求经过P、C两点的直线解式。
(2)  求ΔNPB的面积。
求ΔNPB的面积。
(3) 求Sin∠BPN的值。
6、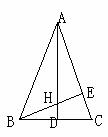 如图,ΔABC中,AB=AC,高AD、BE相交于点H,AH=8,DH=1,求tanC
如图,ΔABC中,AB=AC,高AD、BE相交于点H,AH=8,DH=1,求tanC
5、 在ΔABC中,∠C=90°,∠A的平分线交BC于D,则
在ΔABC中,∠C=90°,∠A的平分线交BC于D,则 ( )
( )
(A)sinA (B)cosA
(C)tgA (D)ctgA
4、在 ABC中,
ABC中, =
= ,且
,且 则下列关系式中,不正确的式子是( )
则下列关系式中,不正确的式子是( )
A.sinA=cosB B. C.tan
C.tan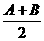 = 1
D. cotA=cotB
= 1
D. cotA=cotB
3、当 为锐角,且sinA的值大于
为锐角,且sinA的值大于 时,
时, 的度数 ( )
的度数 ( )
A.小于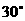 B. 大于
B. 大于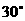 C. 小于
C. 小于 D. 大于
D. 大于
2、在 ABC中,
ABC中, =
= ,BC= a,
,BC= a,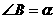 ,则高AD等于 (
)
,则高AD等于 (
)
A. B.
B. C.
C.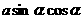 D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com