
题目列表(包括答案和解析)
1、已知 =2,则下列四个式子中一定正确的是( )
=2,则下列四个式子中一定正确的是( )
A、x=2 B、 x=-2 C、 x2=4 D、x3=8
24.(本题满分12分)
在 中,
中, ,
, .以
.以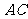 上的点
上的点 为圆心、
为圆心、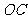 为半径的圆与
为半径的圆与 相切于点
相切于点 ,交
,交 于
于 .过点
.过点 作⊙
作⊙ 的切线,切点为
的切线,切点为 .过点
.过点 作
作 的垂线,垂足为
的垂线,垂足为 ,交⊙
,交⊙ 于
于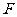 ,
,
(1)求证:四边形 是正方形;
是正方形;
(2)求⊙ 的半径;
的半径;
 (3)连结
(3)连结 、
、 、
、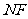 ,在五边形
,在五边形 的5条边中,若从相等关系考虑,你能得到哪些结论?请给出证明.
的5条边中,若从相等关系考虑,你能得到哪些结论?请给出证明.
|
23.(本题满分10分)
行驶中的汽车,在刹车后由于惯性的作用,还要继续向前滑动一段距离才停止,这段距离称为“刹车距离”.为了测定某种型号汽车的刹车性能(车速不超过130km/h),对这种汽车进行测试,测得数据如下表:
|
刹车时车速(km/h) |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
|
刹车距离(m) |
0 |
1.1 |
2.4 |
3.9 |
5.6 |
7.5 |
9.6 |
11.9 |
(1)以车速为x轴,刹车距离为y轴,在下面的方格图中建立坐标系,描出这些数据所表示的点,并用平滑曲线联接这些点,得到函数的大致图像.
(2)观察图像,估计该函数的类型,并确定一个满足这些数据的函数解析式;
(3)该型号汽车在国道上发生了一次交通事故,现测得刹车距离为26.4m.问在事故发生时,汽车是超速行驶还是正常行驶?请说明理由.

22.(本题满分8分)
(1)如图,是边长为1的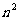 (
( 为大于1的整数)个连续小正方形所组成的图形.
为大于1的整数)个连续小正方形所组成的图形.


……
4个小正方形 9个小正方形
它们经过适当分割(指只用剪刀沿直线剪开,不借助于其它任何工具)后都能拼成一个大正方形,其分割线(图中实线)的最少条数与小正方形的个数之间关系见下表,请填写下表中的空白处:
|
小正方形的个数 |
4 |
9 |
16 |
… |
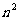 |
|
分割线的最少条数 |
1 |
2 |
|
… |
|

 (2)如图,边长为1的5个连续小正方形所组成的图形按(1)中的要求经过4次分割后也能拼成一个大正方形,其拼成后的图形见方格纸。
(2)如图,边长为1的5个连续小正方形所组成的图形按(1)中的要求经过4次分割后也能拼成一个大正方形,其拼成后的图形见方格纸。

5个小正方形 10个小正方形
边长为1的10个连续小正方形组成的图形,是否
也能够按(1)中的要求经过适当分割后拼成一个大正
方形呢?如果能,则分割线的最少条数为 条。
请在上图中画出分割线,并将分割后拼成的大正方形
画在方格纸中。
(3)你是否还能举出一种非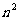 (
( 为大于1的整数)个
为大于1的整数)个
连续小正方形所组成的图形,按(1)中的要求经过适当
分割后能拼成一个大正方形呢?试试看!
连续小正方形的个数为 个,分割线的最少条数为 条。
21.(本题满分7分)
某手机生产厂家根据其产品在市场上的销售情况,决定对原来以每部2000元出售的一款彩屏手机进行调价,并按新单价的八折优惠出售,结果每部手机仍可获得实际销售价的20%的利润(利润=销售价-成本价).已知该款手机每部成本价是原销售单价的60%.
(1)求调整后这款彩屏手机的新单价是每部多少元?让利后的实际销售价是每部多少元?
(2)为使今年按新单价让利销售的利润不低于20万元,今年至少应销售这款彩屏手机多少部?
20.(每小题满分6分,共24分)
(1)“三等分一个角”是数学史上一个著名问题,今天人们已经知道,仅用圆规和直尺是不可能作出的.在探索中,有人曾利用过如下的图形.
 其中,四边形
其中,四边形 是矩形,
是矩形,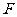 是
是 延长线上一点,
延长线上一点, 是
是 上一点,并且
上一点,并且 ,你能证明
,你能证明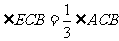 吗?
吗?
(2)某工厂下设甲、乙两个分厂。总厂要评估各分厂的生产效率,并据此来提高职工奖金,下表给出了甲、乙两分厂的产量情况.
|
|
甲 厂 |
乙 厂 |
||
|
产量(只) |
工人数(人) |
产量(只) |
工人数 |
|
|
新车间 |
700000 |
140 |
600000 |
100 |
|
老车间 |
120000 |
60 |
210000 |
100 |
甲厂的负责人说:我工厂人数与乙厂相同,总产量比乙厂高,应该率先提高工人奖金,你同意他的说法吗?为什么?
(3)已知关于x的方程 有两个不相等的实数根
有两个不相等的实数根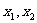 .
.
① 求k的取值范围;
② 是否存在实数k,使方程的两实数根互为相反数?如果存在,求出k的值;如果不存在,请说明理由.
解:①根据题意,得 Δ=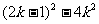 ,
,
又∵方程有两个不相等的实数根,∴Δ>0,即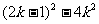 >0,解得
k<
>0,解得
k< 。
。
∴ k的取值范围为k< .
.
② 存在. 如果方程的两实数根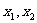 互为相反数,则
互为相反数,则
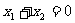 ,
,
又  ,∴
,∴ ……………………(﹡)
……………………(﹡)
解得  . 经检验
. 经检验 是方程(﹡)的解.
是方程(﹡)的解.
∴当 时,方程的两实数根
时,方程的两实数根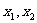 互为相反数.
互为相反数.
读了上面的解答过程,请判断是否有错误?如果有,请指出错误之处,并直接写出正确答案.
|
座位号 |
|
|
(4)如图(天平均处于平衡状态),共有四种物品:烧杯、烧瓶、量筒、砝码.仔细观察并算一算几个烧杯才能跟一个烧瓶平衡?

19.(每小题满分5分,共15分)
(1)解不等式: ≤
≤ .
.
(2)将多项式 分解因式.
分解因式.
(3)已知 是方程
是方程 的一个根,求
的一个根,求 的值和方程其余的根.
的值和方程其余的根.
18.我市出租车收费标准如下:
 起租费:5元;基价里程:3公里;
起租费:5元;基价里程:3公里;
等时费:每等5分钟加收1公里的租价;
租 价:每公里1.20元.
星期天,某同学从家出发坐出租车去新浦
火车站接一朋友回家.如图,表示该同学离家
时间与所行路程之间的关系,则该同学最少应付车
费 元.(注:1公里=1千米)

17.
 一个学生荡秋千,秋千链子的长度为
一个学生荡秋千,秋千链子的长度为 ,当秋千向两边摆动时,摆角(指摆到最高位置时的秋千与铅垂线的夹角)恰好是
,当秋千向两边摆动时,摆角(指摆到最高位置时的秋千与铅垂线的夹角)恰好是 ,则它摆至最高位置时与其摆至最低位置时的高度之差为
,则它摆至最高位置时与其摆至最低位置时的高度之差为  .
.
(结果可以保留根号)
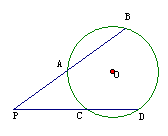
16. 已知:如图,
已知:如图,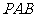 、
、 是⊙
是⊙ 的割线,
的割线, ,
, ,
, .则
.则 =
=
 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com