6．下面四个方程中，两根之和为2的是(　 )

　　 A．x²-2x+4=0　　 B．x²+2x-4=0　　 C．x²-2x-4=0　　 D．x²+2x+4=0

5．下面是某同学在九年级期中测试中解答的几道填空题：(1)若x²=a²，则x= a ；

(2)方程2x(x-1)=x-1的根是 x=0 ；(3)若直角三角形的两边长为3和4，则第三边的长为 5 ．其中答案完全正确的题目个数为(　 )

　　 A．0　　 B．1　　 C．2　　 　D．3

4．要使方程(a-3)x²+(b+1)x+c=0是关于x的一元二次方程，则(　 )

　　 A．a≠0　　　　　 　　　B．a≠3

　　 C．a≠1且b≠-1　 　　D．a≠3且b≠-1且c≠0

3．已知y=x²-5x-6，要使y的值为0，x的取值为(　 )

　　 A．2或-3　　 B．-2或3　　 C．6或-1　　 D．-6或1

2．用配方法解下列方程时，配方有错误的是(　 )

　　 A．x²-2x-99=0化为(x-1)²=100　　 B．2t²-7t-4=0化为(t-)²=

　　 C．x²+8x+9=0化为(x+4)²=25　 　　D．3x²-4x-2=0化为(x-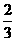)²=

1．(x-3)²=x-3的解为(　 )

　　 A．x=2　　 B．x=4　　 C．x=3　　 D．x=3或x=4

(2)在△ABC 中，∠A=90⁰,AB=6,AC=8. 点P从A开始沿AC向C匀速运动，点Q从点A开始沿AB边点B,再沿BC向点C匀速运动。若P、Q两点同时从点A出发，则可同时到达C.

⑴如果P、Q两点同时从点A出发，以原速度按各自的移动路线移动到某一时刻同时停止移动，当点Q移动到BC边上(Q不与C重合)，求作以tan∠QCA, tan∠QPA为根的一元二次方程。

⑵如果P、Q两点同时从点A出发，以原速度按各自的移动路线移动到某一时刻，同时停止移动，当S△PBQ=, 求PA的长。(本题13分)　　　　　　　 B

　　　　　　　　　　　　　　　　　　　　　　　　　　 A　　　　　　　　 C

3、若m:n=(x+y):(x－y)，且m≠n，　 求x²:y².(用m、n表示)

2、已知a、b为不相等的两个实数，且2a²=5－3a, 2b²=5－3b, 求(a－2)(b－2)的值。

1、方程x²－2ax+a²－4=0的两根都是正数，且大根是小根的5倍，求这两根及a的值。