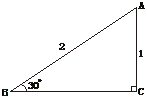
23.(6分)要求tan30°的值，可构造如图6所示的直角三角形进行计算：作Rt△ABC，使∠C=90°，斜边AB=2，直角边AC=1，那么BC=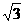，∠ABC=30°，tan30°= ==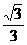.在此图的基础上通过添加适当的辅助线，可求出tan15°的值.请你写出添加辅助线的方法，并求出tan15°的值.

22.(6分)如图5，河岸护堤AD、BC互相平行，要测量河两岸相对两树A、B的距离，小赵从B点沿垂直AB的BC方向前进，他手中有足够长的米尺和含有30°角的一块三角板.

(1)请你帮小赵设计一下测量AB长的具体方案;

(2)给出具体的数值，求出AB的长.

21.(5分)一艘轮船从西向东航行，上午10时航行到点A处，此时测得在船北偏东30°上有一灯塔B，到11时测得灯塔B正好在船的正北方向，此时轮船所处位置为C点 (如图4)，若该船的航行速度为每小时20海里，那么船在C点时距离灯塔B多远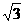？(取1.73)

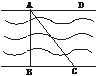
图3　 　　　　　　　　　　　　　　　　　　　　　　　 　　 图4　 　　　　　　　　　　　　　　　　　　 　　 图5

20.(6分)如图3，在Rt△ABC中，∠C=90°，D是BC边上一点，AC=2，CD=1，设　　　　 ∠CAD=α.

　(1)求sinα、cosα、tanα的值;

(2)若∠B=∠CAD，求BD的长.

19.(5分)在Rt△ABC中，∠BCA=90°，CD是中线，AC=6，CD=5，求sinACD、cosACD和tanACD.

18.(8分)根据下列条件，求出Rt△ABC(∠C=90°)中未知的边和锐角.

(1)BC=8，∠B=60°.

(2)∠B=45°，AC=.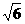

17.(16分)计算或化简：

(1)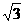cos30°+sin45°;

(2)·tan 30°;

(3)(sin60°+cos 45°)(sin 60°－cos 45°);

(4)6tan² 30°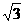－sin 60°－2sin 45°;

16.把Rt△ABC的三边都扩大十倍，关于锐角A的正弦值：甲同学说扩大十倍；乙同学说不变；丙同学说缩小十倍.那么你认为正确的说法应是

A.甲　　　　　　　　 B.乙　　　　　　　　 C.丙　　　 　　　　　 　　D.都不正确

15.在△ABC中，若tanA=1，sinB=，你认为最确切的判断是

A.△ABC是等腰三角形　　　　　　　　　　 B.△ABC是等腰直角三角形

C.△ABC是直角三角形　　　　　　　　　　 D.△ABC是一般锐角三角形

14.李红同学遇到了这样一道题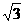：tan(α+20°)=1，你猜想锐角α的度数应是

A.40°　　　　　　　 B.30°　　　　　　　 C.20°　　　　　　 D.10°