
题目列表(包括答案和解析)
2.设OM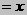 ,AN=
,AN= ,求
,求 关于
关于 的函数解析式,并写出自变量
的函数解析式,并写出自变量 的取值范围;
的取值范围;
|
|
|
|
|
|
|
|
|
|










 3.当以A、F、N为顶点的三角形与△ADE相似时,求直线MN的解析式。
3.当以A、F、N为顶点的三角形与△ADE相似时,求直线MN的解析式。
|
练4.如图9(绵阳市),在平行四边形ABCD中,AD=4 cm,∠A=60°,BD⊥AD. 一动点P从A出发,以每秒1 cm的速度沿A→B→C的路线匀速运动,过点P作直线PM,使PM⊥AD .
(1) 当点P运动2秒时,设直线PM与AD相交于点E,求△APE的面积;
(2) 当点P运动2秒时,另一动点Q也从A出发沿A→B→C的路线运动,且在AB上以每秒1 cm的速度匀速运动,在BC上以每秒2 cm的速度匀速运动. 过Q作直线QN,使QN∥PM. 设点Q运动的时间为t秒(0≤t≤10),直线PM与QN截平行四边形ABCD所得图形的面积为S cm2 .
① 求S关于t的函数关系式;
② (附加题) 求S的最大值.
1.证明:∠OMD=∠ADN;
37、
某人沿着坡比 的山坡向上走了5米,这是他离水平地面有多高?
的山坡向上走了5米,这是他离水平地面有多高?
36、
已知 ,且
,且 ,求
,求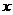 的取值范围。
的取值范围。
35、 直角三角形两直角边的比为7:24,求较小角的余弦值。
34、
已知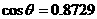 ,查得的
,查得的 修正值为0.0003,则
修正值为0.0003,则 等于多少度?
等于多少度?
33、
当 时,试比较
时,试比较 的大小。
的大小。
32、
已知 的斜边AB长为10,它的两锐角的正弦值是方程
的斜边AB长为10,它的两锐角的正弦值是方程 的两根;(1)求实数
的两根;(1)求实数 的值;(2)求
的值;(2)求 两直角边的长。
两直角边的长。
31、
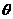 为锐角,判断关于
为锐角,判断关于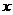 的方程
的方程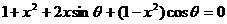 的根的情况。
的根的情况。
30、
若 求
求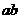 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com