
题目列表(包括答案和解析)
1.若a≠0,则下列运算正确的是( )
(A)试题详情
2.解⑴C(2a,0),……………………………………………1分
D(0,2a+8)………………………………………………………………2分
⑵方法一:由题意得:A(-4,0),B(0,4)
-4<a<0,且a≠2,………………………………………………………………3分
① 当2a+8<4,即-4<a<-2时
AC=-4-2a,BD=4-(2a+8)=-4-2a
∴AC=BD……………………………………………………………………………5分
② 当2a+8>4,即-2<a<0时
同理可证:AC=BD
综上:AC=BD……………………………………………………………………………6分
方法二:①当点D在B、O之间时,
连CD,∵∠COD=90°
∴圆心M在CD上,………………………………………………………………3分
过点D作DF∥AB,
∵点M为CD中点,
∴MA为△CDF中位线,
∴AC=AF,…………………………………………………………………………4分
又DF∥AB,
∴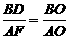 ,
,
而BO=AO
∴AF=BD
∴AC=BD……………………………………………………………………………5分
②点D在点B上方时,同理可证:AC=BD
综上:AC=BD…………………………………………………………………………6分
⑶方法一
①A(-4,0),B(0,4),D(0,2a+8),M(a,a+4),△BDE、△ABO均为等腰直角三角形,
E的纵坐标为a+6,∴ME= (yE-yM)=
(yE-yM)= [a+6-(a+4)]=2
[a+6-(a+4)]=2 …………………7分
…………………7分
AB=4 …………………………………………………………………………8分
…………………………………………………………………………8分
∴AB=2ME…………………………………………………………………………9分
②AM= ( yM-yA)=
( yM-yA)= (a+4),BE=
(a+4),BE= |yE-yB|=
|yE-yB|= |a+2|,……………………10分
|a+2|,……………………10分
∵AM=BE
又-4<a<0,且a≠2,
10 当-4<a<-2时
 (a+4)= -
(a+4)= - (a+2)
(a+2)
∴a=-3
M(-3,1)………………………………………………………………………11分
20 当-2<a<0时
 (a+4)=
(a+4)=  (a+2)
(a+2)
∴a不存在………………………………………………………………………12分
方法二:
①当点D在B、O之间时,作MP⊥x轴于点P、MQ⊥y轴于点Q,取AB中点N,
在Rt△MNO与Rt△DEM中,MO=MD
∠MON=450-∠MOP
∠EMD=450-∠DMQ=450-∠OMQ=450-∠MOP
∴∠MON=∠EMD
∴Rt△MNO≌Rt△DEM………………………………………………………………7分
∴MN=ED=EB
∴AB=2NB=2(NE+EB)=2(NE+MN)=2ME…………………………8分
当点D在点B上方时,同理可证………………………………………………9分
②当点D在B、O之间时,
由①得MN=EB,
∴AM=NE ……………………………………………………………………10分
若AM=BE,则AM=MN=NE=EB=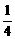 AB=
AB=
∴M(-3,1)……………………………………………………………………11分
点D在点B上方时,不存在。…………………………………………………12分
注:(2)、(3)两问凡需要讨论而没有讨论的,每漏讨论一次扣1分。
1.
.解:(1)S△PCQ= PC·CQ=
PC·CQ= =
= =2, ………1分
=2, ………1分
解得 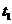 =1,
=1, =2
………2分
=2
………2分
∴当时间 为1秒或2秒时,S△PCQ=2厘米2; ………3分
为1秒或2秒时,S△PCQ=2厘米2; ………3分
(2)①当0< ≤2时,S=
≤2时,S=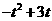 =
= ; ………5分
; ………5分
②当2< ≤3时, S=
≤3时, S=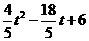 =
= ;………7分
;………7分
③当3< ≤4.5时,S=
≤4.5时,S= =
= ;…9分
;…9分
(3)有; ………10分
①在0< ≤2时,当
≤2时,当 =
= ,S有最大值,S1=
,S有最大值,S1= ; ………11分
; ………11分
②在2< ≤3时,当
≤3时,当 =3,S有最大值,S2=
=3,S有最大值,S2= ; ………12分
; ………12分
③在3< ≤4.5时,当
≤4.5时,当 =
=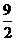 ,S有最大值,S3=
,S有最大值,S3= ; ………13分
; ………13分

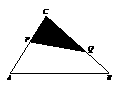
 ∵S1<S2<S3 ∴
∵S1<S2<S3 ∴ =
=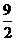 时,S有最大值,S最大值=
时,S有最大值,S最大值= . ………14分
. ………14分
3.解、解:(1)设直线AB的解析式为y=kx+b
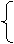 由题意,得 b=6
由题意,得 b=6
8k+b=0
解得 k=- b=6
b=6
 所以,直线AB的解析式为y=-
所以,直线AB的解析式为y=- x+6. ………2分
x+6. ………2分
(2)由 AO=6, BO=8 得 AB=10
所以AP=t ,AQ=10-2t
1° 当∠APQ=∠AOB时,△APQ∽△AOB.
所以  =
= 解得 t=
解得 t=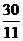 (秒) ………4分
(秒) ………4分
2° 当∠AQP=∠AOB时,△AQP∽△AOB.
所以  =
= 解得 t=
解得 t= (秒) ………6分
(秒) ………6分
(3)过点Q作QE垂直AO于点E.
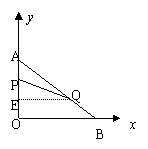 在Rt△AOB中,Sin∠BAO=
在Rt△AOB中,Sin∠BAO= =
= …………7分
…………7分
在Rt△AEQ中,QE=AQ·Sin∠BAO=(10-2t)· =8-
=8- t
t
所以,S△APQ= AP·QE=
AP·QE= t·(8-
t·(8- t)
t)
=-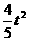 +4t=
+4t=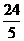 ……………………9分
……………………9分
解得t=2(秒)或t=3(秒). ……………………10分
(注:过点P作PE垂直AB于点E也可,并相应给分)
2.2005年无锡市
解、(1)证∠APE=∠ADQ,∠AEP=∠AQD.
(2)注意到△APE∽△ADQ与△PDE∽△ADQ,及S△PEF= ,得S△PEF=
,得S△PEF=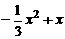 =
= . ∴当
. ∴当 ,即P是AD的中点时,S△PEF取得最大值
,即P是AD的中点时,S△PEF取得最大值 .
.
 (3)作A关于直线BC的对称点A′,连DA′交BC于Q,则这个点Q就是使△ADQ周长最小的点,此时Q是BC的中点.
(3)作A关于直线BC的对称点A′,连DA′交BC于Q,则这个点Q就是使△ADQ周长最小的点,此时Q是BC的中点.
1. 解:(1)不变. ………………………………………………………………1分
理由:在直角三角形中,斜边上的中线等于斜边的一半,因为斜边AB不变,所以斜边上的中线OP不变. ………3分
 (2)当△AOB的斜边上的高h等于中线OP时,△AOB的面积最大. ………………………………4分
(2)当△AOB的斜边上的高h等于中线OP时,△AOB的面积最大. ………………………………4分
如图,若h与OP不相等,则总有h<OP,
故根据三角形面积公式,有h与OP相等时△AOB的面积最大. …………………………………5分
此时,S△AOB= .
.
所以△AOB的最大面积为 . ……………6分
. ……………6分
1.点在直线上运动
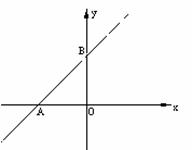
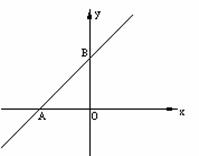
2.如图,已知直线y=x+4与x轴、y轴分别相交于点A、B,点M是线段AB(中点除外)上的动点,以点M为圆心,OM的长为半径作圆,与x轴、y轴分别相交于点C、D.
(1)设点M的横坐标为a,则点C的坐标为 ,点D的坐标为 (用含有a的代数式表示);
(2)求证:AC=BD;
(3)若过点D作直线AB的垂线,垂足为E.
①求证: AB=2ME;
②是否存在点M,使得AM=BE?若存在,求出点M的坐标;若不存在,请说明理由.
(3).(重庆市2005)如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
(1) 求直线AB的解析式;
(2) 当t为何值时,△APQ与△AOB相似?
(3) 当t为何值时,△APQ的面积为 个平方单位?
个平方单位?

练习
1.(分类讨论题)
已知:如图,△ABC中,∠C=90°,AC=3厘米,CB=4厘米.两个动点P、Q分别从A、C两点同时按顺时针方向沿△ABC的边运动.当点Q运动到点A时,P、Q两点运动即停止.点P、Q的运动速度分别为1厘米/秒、2厘米/秒,设点P运动时间为 (秒).
(秒).
(1)当时间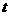 为何值时,以P、C、Q三点为顶点的三角形的面积(图中的阴影部分)等于2厘米2;
为何值时,以P、C、Q三点为顶点的三角形的面积(图中的阴影部分)等于2厘米2;
(2)当点P、Q运动时,阴影部分的形状随之变化.设PQ与△ABC围成阴影部分面积为S(厘米2),求出S与时间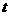 的函数关系式,并指出自变量
的函数关系式,并指出自变量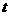 的取值范围;
的取值范围;
 (3)点P、Q在运动的过程中,阴影部分面积S有最大值吗?若有,请求出最大值;若没有,请说明理由.
(3)点P、Q在运动的过程中,阴影部分面积S有最大值吗?若有,请求出最大值;若没有,请说明理由.
(1)(2005年北京市)
 如图所示,一根长2a的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,设木棍的中点为P. 若木棍A端沿墙下滑,且B端沿地面向右滑行.
如图所示,一根长2a的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,设木棍的中点为P. 若木棍A端沿墙下滑,且B端沿地面向右滑行.
(1)请判断木棍滑动的过程中,点P到点O的
距离是否变化,并简述理由.
(2)在木棍滑动的过程中,当滑动到什么位置时,△AOB的面积最大?简述理由,并求出面积的最大值.
(2)、(2005年无锡市)
如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P异于A、D),Q是BC边上的任意一点. 连AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.
(1)求证:△APE∽△ADQ;
(2)设AP的长为x,试求△PEF的面积S△PEF关于x的函数关系式,并求当P在何处时,S△PEF取得最大值?最大值为多少?
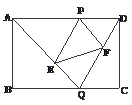 (3)当Q在何处时,△ADQ的周长最小?(须给出确定Q在何处的过程或方法,不必给出证明)
(3)当Q在何处时,△ADQ的周长最小?(须给出确定Q在何处的过程或方法,不必给出证明)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com