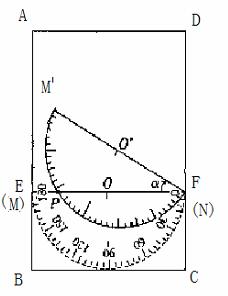
29．(本题7分) 如图，在矩形ABCD中，AB=3，AD=2，点E、F分别在AB、DC上，AE=DF=2.再把一块直径为2的量角器(圆心为O)放置在图形上，使其0°线MN与EF重合；若将量角器0°线上的端点N固定在点F上，再把量角器绕点F顺时针方向旋转∠α(0°<α<90°),此时量角器的半圆弧与EF相交于点P，设点P处量角器的读数为°.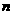

(1)用含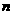°的代数式表示∠α的大小；

(2)当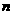°等于多少时，线段PC与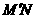平行？

28．(本题9分) 某地区为了改善生态环境，防止水土流失，决定从2003年起开始“退耕还林”，在山坡上推广种植某种果树，并且出台了一项激励措施：在“退耕还林”的过程中，每一年新增果树达到100棵的农户，当年都可得到生活补贴1200元，且每超出一棵，政府还给予每棵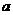元的奖励．另外，种植的果树，从下一年起，每年每棵平均将有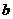元的果实收入．

下表是某农户在头两年通过“退耕还林”每年获得的总收入情况：

(注：年总收入＝生活补贴费+政府奖励费+果实收入)

(1)试根据以上提供的资料确定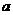、的值；

(2)从2005年起，该农户每年新增果树的棵数将以某一百分率增长，预计2006年新增果树216棵，那么2006年该农户通过“退耕还林”获得的年总收入将达到多少元？

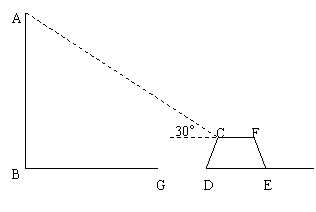
27．(本题7分)城市规划期间，欲拆除一电线杆AB(如图)，已知与电线杆AB水平距离14米的D处有一等腰梯形大坝CDEF，该梯形的上底CF长为3米，下底DE长为5米，

∠CDE=60°，在坝顶C处测得杆顶A的仰角为30°,D、G之间是宽3米的人行道．试问：在拆除电线杆AB时，为确保行人安全，是否需要将此人行道封闭?请说明理由．(在地面上，以点B为圆心，以AB长为半径的圆形区域为危险区域)

26.(本题7分) 如图，正方形ABCD的边CD在正方形ECGF的边CE上，连结BE、DG.

　 (1) 观察猜想BE与DG之间的大小关系，并证明你的结论;

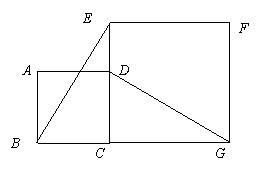　 (2) 图中是否存在通过旋转能够互相重合的两个三角形? 若存在，请说出旋转过程; 若不存在，请说明理由.

25．(本小题5分) 解方程：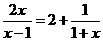

24．(本小题5分)

先化简代数式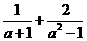，然后再选取一个使原式有意义，你又喜欢的数代入求值：

23．(本小题5分)计算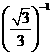： －sin6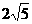0°+(－)⁰－．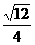

22． 如图，在边长为2的正方形内部，以各边为直径画四个半　　　　　　　圆，则图中阴影部分的面积是　　．

21．如图，平行四边形ABCD的周长为16cm，AC、BD相交于点O，OE⊥AC交AD于E，则△DCE的周长为__________㎝

20．一跳蚤在一直线上从O点开始，第1次向右跳1个单位，紧接着第2次向左跳2个单位，第3次向右跳3个单位，第4次向左跳4个单位，……，依此规律跳下去，当它跳第100次落下时，落点处离O点的距离是　　　　 个单位.