
题目列表(包括答案和解析)
例题(19)、如图(2-1),P为正三角形外一点,且不与A、B在同一直线上,AP=2,BP=3,当此三角形的边长、位置都可改变时,PC的长能否取到最大值?若能取到,求出这个最大值;若不能取到,请说明理由。
解:把△APB绕点A顺时针旋转600,使AB与AC重合,得△ACP1,连结PP1,则△APP1是正三角形,PP1=AP=AP1=2,P1C=PB=3,当P、P1、C不在一直线上时, PC<PP1+P1C=2+3=5,只有当P、P1、C在一直线上时,PC之间的距离在到最大值,

这个最大值是PP1+P1C=5。
例题(18)、已知X1,X2,X3,X4,X5,X6,X7 为自然数,且X1 < X2<X3< …<X6<X7,又X1+X2+…+X6+X7 = 159,则X1+X2+X3的最大值是-------- 。
解:∵X1<X2<
… <X6<X7 ,且它们均是自然数,∴X7≥X6+1≥ …≥X2+5≥X1+6;X6≥X1+5,…,X2≥X1+1;∴7X1+(1+2+…+5+6)≤X1+X2+…+X6+X7 = 159,∴7X1≤138,X1≤19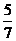 ,∴X1的最大值是 19。同理6X2+(1+2+…+5)≤X2+X3+…+X7 = 140,∴X2≤20,X2的最大值是20;…,
X3的最大值是22。∴X1+X2+X3的最大值是 61 。
,∴X1的最大值是 19。同理6X2+(1+2+…+5)≤X2+X3+…+X7 = 140,∴X2≤20,X2的最大值是20;…,
X3的最大值是22。∴X1+X2+X3的最大值是 61 。
例题(17)、已知三个非负数a、b、c满足3a+2b+c = 5,2a+b-3c = 1,若Q = 3a+b-7c ,求Q的最大和最小值。
解:由已知条件3a+2b+c=5 ,2a+b-3c=1得a = 7c-3,b = -11c+7,∴Q = 3c-2,从而 c = 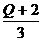 . ∵a、b都是非负数,∴7c-3 ≥0,-11c+7≥ 0,
. ∵a、b都是非负数,∴7c-3 ≥0,-11c+7≥ 0, 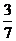 ≤c ≤
≤c ≤ 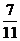 , ∴-
, ∴-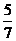 ≤Q ≤-
≤Q ≤-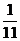 . ∴Q的最大值是-1/11,Q的最小值是-5/7。
. ∴Q的最大值是-1/11,Q的最小值是-5/7。
[本例先用c代换a、b ,根据非负数性质确定c的允许值范围,在c 的约束下求Q的值域,确定Q的最大、最小值。]
例题(15)、若│y│≤1,且2x+y = 1.则2x2+16x+3y2的最小值是------。
解:∵∣y∣≤1,∴-1≤y≤1,由2x+y=1得y=1-2x,即-1≤1-2x≤1,∴0≤x≤1.
又∵y=1-2x,∴y2=4x2-4x+1,∴2x2+16x+3y2 = 14x2+4x+3 = 14(x+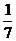 )2+
)2+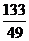 . ∵0≤x≤1,而二次函数的图像对称轴是直线x=-
. ∵0≤x≤1,而二次函数的图像对称轴是直线x=-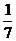 ,在对称轴的右侧,y随x增大而增大,∴当x=0时,原代数式的最小值是3 。(当x=1时有最大值21。
,在对称轴的右侧,y随x增大而增大,∴当x=0时,原代数式的最小值是3 。(当x=1时有最大值21。
例题(16)、设m是不小于-1的实数,使得关于X的方程X2+2(m-2)X+m2-3m+3 =
0 有两个不相等的实数根X1,X2
。求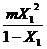 +
+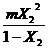 的最大值。
的最大值。
解:∵原方程有两个不相等的实数根,∴⊿ > 0,解得m < 1,且已知m是不小于-1的实数,∴-1≤ m < 1 。
由韦达定理得:X1+X2 = 2(2 – m), X1·X2 = m2-3m+3 ,
y = 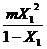 +
+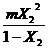 =
=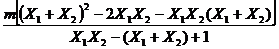 =2(m2-3m+1)=2(m -
=2(m2-3m+1)=2(m -  )2-
)2-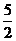 .y是关于m的二次函数,对称轴为直线m =
.y是关于m的二次函数,对称轴为直线m = ,在对称轴左侧,y随m的增大而减小,因为-1≤m< 1 ,所以当m = -1时,y的最大值是10,∴原代数式的最大值是10 。
,在对称轴左侧,y随m的增大而减小,因为-1≤m< 1 ,所以当m = -1时,y的最大值是10,∴原代数式的最大值是10 。
[说明:二次函数最值的确定,要根据自变量的取值范围来确定,当自变量的变化范围是一个闭区间时,它一定有最大和最小值,若是半闭半开区间时,它只能有一个最大或最小值,这个最值不一定在顶点取得;若是开区间则由顶点位置确定最值。]
例题(12)已知0≤a≤4,那么┃a-2┃+┃3-a┃的最大值等于( )
A. 1 B. 5 C. 8 D. 3
解:根据已知条件采用取零点分段讨论法求最大值。根据绝对值的几何意义,a=2 ,a=3是两个零点,结合0≤a≤4分成0≤a≤2,2<a≤3,3<a≤4三段讨论。1,当0≤a≤2时,原式=5-2a,当a=0时达到最大值5;2,当2<a≤3时,原式=1;3,当3<a≤4时,原式=2a-5,当a=4时达到最大值3;综合123在0≤a≤4上原式的最大值为5 。所以选取B。
例题(13)、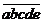 是一个五位自然数,其中a,b,c,d,e为阿拉伯数字,且a<b<c<d ,则│a-b│+│b-c│+│c-d│+│d-e│的最大值是 ---。
是一个五位自然数,其中a,b,c,d,e为阿拉伯数字,且a<b<c<d ,则│a-b│+│b-c│+│c-d│+│d-e│的最大值是 ---。
解:由已知条件a<b<c<d分析,化简本题的关键是化去│d-e│中的绝对值符号。所以分两种情况讨论,当d≤e时,原式=e-a,当e=9,a=1时原式的最大值为8;当d>e时,原式=2d-a-e,当d=9,a=1,e=0时,原式的最大值为17 。所以原式的最大值为17 。
例题(14)、1,求代数式│X-1│+│X-2│+│X-3│+…+│X-2003│的最小值。2,求代数式│X-1│+│X-2│+│X-3│+…+│X-2004│的最小值。
解:1,本题用分段讨论法肯定是不恰当的,也太麻烦了。应该用绝对值的几何意义来解比较妥当。因为│X-1│的意义是:在数轴上表示实数X的点到表示1的点的距离。所以只有当X在表示点1、2、3、…、2003的正中位置时,即当X=1002时,│X-1│+│X-2│+│X-3│+…+│X-2003│的值最小,即原式最小值为1001+1000+999+…+2+1+0+1+2+…+999+1000+1001 = 2(1+2+3+…+1001)= 1003002。2,因为1、2、3、…、2003、2004的正中位置在数1002和1003之间,所以当X在1002≤X≤1003范围内取任意一点值时,原式都能取到最小值。当X=1002或X=1003时原式的值最小。现用X=1002计算,原式的最小值为1001+1000+999+…+2+1+0+1+2+…+1000+1001+1002 = 2(1+2+…+1001)+1002 = 1004004 。
[说明:对于求│X-a1│+│X-a2│+│X-a3│+│X-an│型代数式的最小值,有如下结论可以应用:当an是奇数时,在X=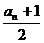 时,代数式的值最小;当an是偶数时,在
时,代数式的值最小;当an是偶数时,在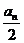 ≤X≤
≤X≤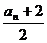 时代数式的值最小。]
时代数式的值最小。]
例题(8)、已知实数a、b、c满足a+b+c = 2 ,abc = 4 ,1求a、b、c中最大者的最小值 ;2求∣a∣+∣b∣+∣c∣的最小值。
解:1,设a为最大者,则由题意得 b+c=2-a,bc=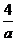 ,由韦达定理得b、c是关于X的二次方程X2-(2-a)X+
,由韦达定理得b、c是关于X的二次方程X2-(2-a)X+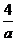 =0的两个实数根。∴Δ=(2-a)2-4×1×
=0的两个实数根。∴Δ=(2-a)2-4×1×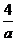 ≥0 ,展开后整理并分解因式得(a2+4)(a-4)≥4 ,∴ a≥4。所以最大数a的最小值是4 。
≥0 ,展开后整理并分解因式得(a2+4)(a-4)≥4 ,∴ a≥4。所以最大数a的最小值是4 。
[即当b=c=-1时a取最小值。划线部份转化为二次方程根与系数关系是关键。另外设a、b、c哪个最大是等价的。]
2、由1知最大数a的最小值为4,所以a、b、c不可能全为正,那么只可能是两负一正,若a为正,则b、c均为负,∴∣a∣+∣b∣+∣c∣= a-b-c = 2a-2≥0 , ∵a≥4, ∴∣a∣+∣b∣+∣c∣≥6 . ∴∣a∣+
∣b∣+∣c∣的最小值是6 。
例题(9)、求函数Y = 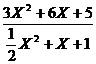 的最小值。
的最小值。
解:原式可化为(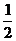 X2+X+1)Y =3X2+6X+5 ,整理得(6-Y)X2+(12-2Y)X+(10-2Y)=0,因为X的取值范围是全体实数,所以关于X的二次方程有实数根,∴Δ = (12-2Y)2-4×(6-Y)(10-2Y)= -4Y2+40Y-96≥ 0 。即Y2-10Y+24≤ 0 ,由(Y-4)(Y-6)≤0 得 4 ≤ Y ≤ 6 。所以Y的最小值为 4 。
X2+X+1)Y =3X2+6X+5 ,整理得(6-Y)X2+(12-2Y)X+(10-2Y)=0,因为X的取值范围是全体实数,所以关于X的二次方程有实数根,∴Δ = (12-2Y)2-4×(6-Y)(10-2Y)= -4Y2+40Y-96≥ 0 。即Y2-10Y+24≤ 0 ,由(Y-4)(Y-6)≤0 得 4 ≤ Y ≤ 6 。所以Y的最小值为 4 。
[说明:本题也可以用以下的方法来做。Y=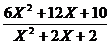 =
=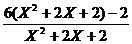 = 6-
= 6-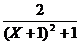 ,当(X2+1)+1最小时,
,当(X2+1)+1最小时,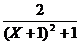 最大,从而得Y最小值是4
。]
最大,从而得Y最小值是4
。]
例题(10)、如图(1-1),在ΔABC中,D、E分别是BC、AB上的点,且∠1=∠2=∠3 ,如果ΔABC、ΔEBD、ΔADC的周长依次为m,m1,m2,求证: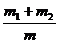 的最小值是
的最小值是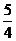 。
。
证明:由∠1=∠2,∠C是公共角,得ΔABC∽ΔDAC, 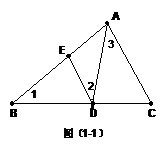
∴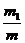 =
=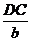 =
=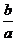 , DC=
, DC=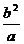 ,∵∠2=∠3得DE∥AC,∴ΔBDE∽ΔBCA,∴
,∵∠2=∠3得DE∥AC,∴ΔBDE∽ΔBCA,∴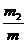 =
=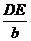 =
=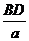 ,而
,而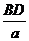 =
=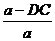 =
= = 1-(
= 1-(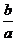 )2 。令K=
)2 。令K=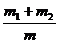
则 K =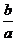 +1-(
+1-(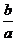 )2,即(
)2,即(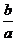 )2-
)2-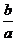 +K-1= 0, ∵ a、b 为实数, ∴⊿ =
+K-1= 0, ∵ a、b 为实数, ∴⊿ =
(-1)2-4(K-1)≥ 0 ,得K≤ 4 。∴ 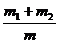 的最小值为4 。
的最小值为4 。
例题(11)已知矩形A的边长分别为a、b,如果总有另一矩形B,使得矩形B与矩形A的周长之比和面积之比都等于K。试问K是否存在最小值,若存在,求出这个最小值;若不存在,请说明理由。
解:K存在最小值。设矩形B的边长分别为m、n ,根据题意得: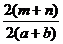 =K,
=K,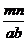 =K,∴m+n =K(a+b),mn = Kab ;则m、n 是关于X的方程X2-K(a+b)X+Kab = 0的两个根。必须满足⊿=K2(m+n)-4Kmn≥ 0 ,∵K≠0,∴K≥
=K,∴m+n =K(a+b),mn = Kab ;则m、n 是关于X的方程X2-K(a+b)X+Kab = 0的两个根。必须满足⊿=K2(m+n)-4Kmn≥ 0 ,∵K≠0,∴K≥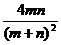 。∴K的最小值是
。∴K的最小值是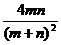 。
。
[说明:二次方程根的判别式往往和韦达定理结合在一起应用]
例题(6)、若X > 0,则函数Y =
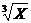 +
+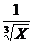 +
+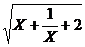 的最小值。
的最小值。
解:原式 = 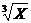 +
+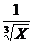 +
+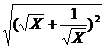 =
= 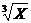 +
+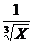 +
+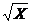 +
+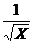 ≥2
≥2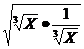 +2
+2 = 2+2 = 4 。所以原式的最小值是 4 。
= 2+2 = 4 。所以原式的最小值是 4 。
[说明:这个公式的来源是由(a-b)2≥0直接推出的。]
例题(7)、已知 a、b、c、d均为实数,且a+b+c+d = 4 ,a2+b2+c2+d2 =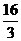 ,求a的最小值与最大值。
,求a的最小值与最大值。
解:∵a+b+c+d = 4 ,
∴b+c+d = 4- a ,
∴ (b+c+d)2 = b2+c2+d2+2bc+2cd+2bd ≤b2+c2+d2+(b2+c2)+(c2+d2)+(d2+b2)=3(b2+c2+d2)
∵b+c+d = 4-a, ∴(b+c+d)2 = (4-a)2 .
∵ a2+b2+c2+d2 = 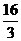 ,
∴b2+c2+d2 =
,
∴b2+c2+d2 = 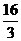 -a2 。
-a2 。
∴ (4-a)2≤ 3×(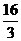 -a2) ,化简得 a(a-2)≤ 0
,解得0≤ a ≤2 。
-a2) ,化简得 a(a-2)≤ 0
,解得0≤ a ≤2 。
∴ a的最小值是0 ,a的最大值是2 。
[说明,本例的关键是划线部份的变换逆用了a2+b2≥2ab,从而达到了把(b+c+d)以及b2+c2+d2都用a替换的目的。]
3、用(a±b)2≥0 ,∣a∣≥0,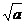 ≥0的方法解题。
≥0的方法解题。
[说明:这里用到的很重要的思想方法是配方法和整体代换思想。]
例题(1)、若实数a ,b ,c 满足a2 + b2 + c2 = 9,则代数式 (a - b)2 + (b -c)2 +(c - a)2的最大值是 ( )
A.27 B、 18 C、15 D、 12
解:(a-b)2+(b-c)2+(c-a)2= 2(a2+b2+c2)-2ab-2bc-2ca = 3(a2+b2+c2)-a2-b2-c2-2ab-2bc-2ca = 3(a2+b2+c2)-(a2+b2+c2+2ab+2bc+2ca) =3(a2+b2+c2)-(a+b+c)2 = 27-(a+b+c)2 ≤ 27 . ∵a2+b2+c2 = 9 , ∴ a,b,c 不全为0 。当且仅当a + b + c = 0 时原式的最大值为 27 。
[说明,本例的关键是划线部份的变换,采用加减(a2+b2+c2)后用完全平方式。]
例题(2)、如果对于不小于8的自然数N ,当3N+1是一个完全平方数时,N + 1都能表示成K个完全平方数的和,那么K的最小值是 ( )
A、 1 B、 2 C、 3 D、 4
解:设 ∵ 3N+1是完全平方数,∴ 设 3N+1 = X2 (N≥ 8),则3不能整除X,所以X可以表示成3P±1的形式。3N+1=(3P±1)2= 9P2±6P+1=3X2±2X+1=X2+X2+(X±1)2。即3N+1能够表示成三个完全平方数的和。所以K的最小值为 3 。选 C 。
[说明,本例的关键是如何把3X2拆成X2+X2+X2,然后配方求解。]
例题(3)、设a、b为实数,那么a2+ab+b2-a-2b的最小值是----------。
解:a2+ab+b2-a-2b = a2+(b-1)a+b2-2b = a2+(b-1)a+(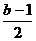 )2+
)2+ b2-
b2- b-
b-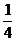 =(a+
=(a+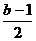 )2+
)2+ (b-1)2-1 ≥ -1 。只有当a+
(b-1)2-1 ≥ -1 。只有当a+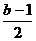 = 0且b-1= 0 时,即a=0,b=1时取等号。所以原式的最小值是-1。
= 0且b-1= 0 时,即a=0,b=1时取等号。所以原式的最小值是-1。
[注意:做这一类题的关键是先按一个字母降幂排列,然后配方。]
例题(4)、已知实数a、b满足a2+ab+b2=1 ,则a2-ab+b2的最小值和最大值的和是-------- 。
解:设a2-ab+b2 = K,与a2+ab+b2
=1联立方程组,解得:a2+b2 = 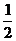 (1+K),ab =
(1+K),ab = 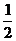 (1-K)。
(1-K)。
∵(a+b)2≥0, ∴a2+b2+2ab=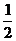 (1+K)+2×
(1+K)+2×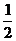 (1-K)≥0, ∴K≤3 . ∵(a-b)2≥0, ∴a2+b2-2ab =
(1-K)≥0, ∴K≤3 . ∵(a-b)2≥0, ∴a2+b2-2ab = 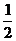 (1+K)-2×
(1+K)-2×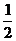 (1-K)≥0, ∴K≥
(1-K)≥0, ∴K≥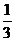 . 得
. 得 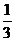 ≤K≤3 。
所以 a2-ab+b2的最小值是
≤K≤3 。
所以 a2-ab+b2的最小值是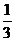 ,最大值是3 ,这两个值的和是3
,最大值是3 ,这两个值的和是3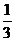 。
。
[本题的关键在于直接运用(a±b)2≥0 ]
例题5、若a、b满足3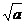 +5∣b∣= 7 ,则S = 2
+5∣b∣= 7 ,则S = 2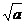 -3∣b∣的最大值为------------------- ,最小值为-------------------- 。
-3∣b∣的最大值为------------------- ,最小值为-------------------- 。
解:联立3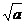 +5|b| = 7和S
= 2
+5|b| = 7和S
= 2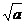 -3|b|两式,解得19
-3|b|两式,解得19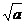 = 21+5S,19|b|=14-3S 。∵ 19
= 21+5S,19|b|=14-3S 。∵ 19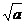 ≥0,∴21+5S≥0,S≥-
≥0,∴21+5S≥0,S≥-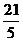 。 ∵19∣b∣≥0,∴14-3S≥0 , ∴S ≤
。 ∵19∣b∣≥0,∴14-3S≥0 , ∴S ≤ , 得 -
, 得 -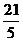 ≤S≤
≤S≤ 。所以S的最大值为
。所以S的最大值为 ,最小值为-
,最小值为-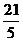 。
。
[说明:这里直接运用了∣a∣≥0和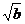 ≥0 ]
≥0 ]
2、若M = -(X±a)2 + b ,则当X±a = 0 时M有最大值b 。
1、若M =(X±a)2 +b ,则当X±a = 0时M有最小值b 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com