8、若M=(X+1)(X+2)(X+3)(X+4)+50，则M的最小值是________ .

7、如果a,b,c是实数，且满足关系式b²+c²=2a²+16a+14与bc=a²－4a－5，那么a的最大值与最小值的和是________ .　　　　 [用(b-c)²≥0]

6、设实数a,b满足　　　 a²－bc－8a+7=0

b²+c²+bc－6a+6=0，则a的最大值与最小值的和是 _{________________} 。　　

[先由原方程组求出b²+c²,bc用a表示的代数式，再由(b－c)²≥0解不等式a²－10a+9≤0求得1≤a≤9,所以a的最大值为9，最小值为1。]

5、四边形ABCD的面积为32，AB、CD、AC的长都是整数，且它们的和为16，1这样的四边形有几个？2这样的四边形边长的平方和的最小值是多少？

[先由AB=a、CD=b、AC=m都是正整数 ,且四边形ABCD面积=三角形ABC面积+三角形ACD面积=1/2ah_a+1/2bh_b≤1/2(a+b)m ,当且仅当h_a=h_b=m时等号成立，这时AB‖CD，即四边形ABCD为平行四边形或梯形，且AC是高。又从(a+b)m≥32,a+b+m=16 得满足条件的四种情况。]

4、求函数Y=X⁴+X²+1的最小值。

[Y=(X²+1)²+，当X=0时Y最小值是1。]

3、设X₁，X₂是关于X的方程X²+aX+a = 2的两个实数根，则(X₁－2X₂)(X₂－2X₁)的最大值为_------ 。

2、已知在直角坐标系中有三点A(0，1)、B(1，3)、C(2，6)，直线Y=aX+b上横坐标为0、1、2的三点为D、E、F，试求a、b的值，使DA²+EB²+FC²取得最小值。

[把D、E、F三点的纵坐标用含a、b的代数式表示，然后把DA²+EB²+FC²用含a、b的二次式表示，配方后求出最小值。当a=5/2,b=5/6,最小什为1/6。]

1、已知：a < 0, b ≤ 0, c > 0 ,且 = b²－2ac ,求b²－4ac的最小值。

[把已知条件两边平方后得ac = b－1,代入b²－4ac就能求得最小值4。]

例题(21)、某蔬菜基地种植西红柿，由历年的市场行情知，从二月一日起的250天内，西红柿的市场售价P与上市时间t的关系用图(3-1)中的一条线段表示；西红柿的种植成本Q与上市时间t的关系可用图(3-2)中的抛物线来表示。(市场售价P和种植成本Q的单位：元/10²kg，时间单位：天 )。若认定“市场售价－种植成本 = 纯收益”，问何时上市的西红柿纯收益最大？

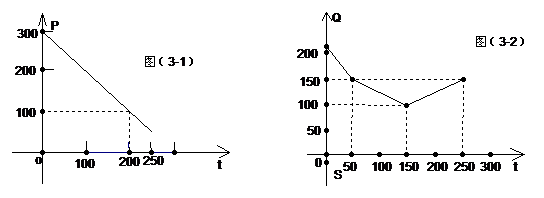
解：如图(3-1)得函数关系式为：P = 300－t (0≤t≤ 250).

　　 如图(3-2)得函数关系式为：Q = (t－150)²+100 (0≤t≤250).

纯收益S = P－Q = －(t－50)²+100 .即从二月一日开始的第50天上市西红柿的纯收益最大。

[说明：此类生活中的数学问题，具有强烈的时代气息，来源于生活生产实际，是近年来各级各类竞赛考试的热门试题，综合性强，知识的涉及点多，知识的应用要求高，在辅导中要引起重视。]

例题(20)、若对于n≥2存在整数a₁,a₂,…,a_n使得 a₁+a₂+…+a_n = a₁a₂…a_n = 1990,则n 的最小值是 _--------　 。

解：由于1990是偶数，且只能被2整除，所以由a₁a₂…a_n=1990知a₁,a₂,…,a_n中只有一个偶数；又由a₁+a₂+…+a_n =1990是偶数知,在a₁,a₂,…,a_n 中有偶数个奇数。因为n≥2，所以n必是大于等于3的奇数。

当n=3时，设a₁≥a₂≥a₃ ,由a₁+a₂+a₃ =1990,知a₁≥,结合a₁a₂a₃ =1990得a₁=1990,或者a₁=995,从而找不到a₂,a₃满足条件；当n = 5 时，可取a₁=1990,a₂=a₃=1,a₄=a₅=－1,满足条件。所以n的最小值是5 。