
题目列表(包括答案和解析)
38、ΔABC中,BC=a,AC=b,以AB为边向ΔABC外作等边ΔABD,问当∠ACB为多少度时,C、D两点的距离最大?最大值是多少?若以AB为边向外作正方形ABDE,问当∠ACB为多少度时,点C到正方形ABDE的中心O的距离最大?最大值是多少?

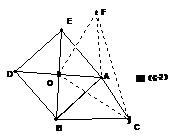
[如图6-1,把△DBC绕点D逆时针旋转600,点B与A重合,得△DAE≌ΔDBC,且ΔDEC是等边三角形,当C、A、E三点共线时,CD的值最大。此时∠ACB=1200,CD的最大值是a+b.在图6-2中,同理可得当∠ACB=900时,CO的最大距离为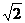 (a+b)。]
(a+b)。]
37、如图,ΔABC的边AB=2,AC=3,ⅠⅡⅢ分别表示以AB、BC、AC为边的正方形,则图中阴影部分面积和的最大值是_______ 。

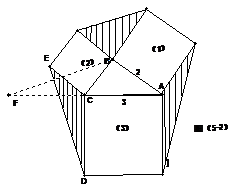
[把三角形ECD绕点C顺时针旋转900,得三角形ECF,点C为FA的中点,ΔBCF的面积=ΔABC的面积,即ΔECF的面积=ΔABC的面积,所以阴影部分面积和=3ΔABC的面积。而ΔABC的面积≤1/2AC·AB,只有当∠BAC=900时等号成立。面积和的最大值为9。]
36、圆周上依次相连排列着十个圆,要将1,2,3,…,10这十个数分别填入十个圆圈内,使任意连续相邻的五个圆圈内的数的和均不大于某个整数M,求M的最小值并完成你的填图。
[根据题意建立不等式组,确定M≤27·5,M的最小值为28,填法有多种:如10,7,6,3,2,9,8,5,4,1就是一种。]
35、在ΔABC中,∠A≤∠C≤∠B,且2∠B=5∠A。求∠B的最大和最小值。
[750,1000]
34、已知x,y,z是三个非负有理数,且满足3x+2y+z=5,x+y+z=2,设 S=2x+y-z,求S的最大和最小值。
[ 把y、z用x表示,然后确定x的取值范围,就可通过解不等式组求S的最值。]
33、已知a,b是正数,抛物线y=x2+ax+2b与y=x2+2bx+a都与x轴有公共点,则a2+b2 的最小值是_________ 。
[当a=4,b=2时,最小值为20。]
32、已知x2+xy+y2=2,求x2-xy+y2 的最大值和最小值。[6,1/3]
31、若a,c,d是整数,b是正整数,且满足a+b=c,b+c=d,c+d=a.那么a+b+c+d的最大值为( )
A. –1 B. –5 C. 0 D. 1 [选B]
30、平面直角坐标系中,有点P(-1,-2)和Q(4,2),取点R(1,m),求当m为何值时,PR+QR有最小值。
[因为点P、Q在直线x=1 的两侧,所以只要求出过点P、Q的直线方程,然后求直线PQ直线x=1的交点坐标 。m=-2/5]
29、在平面直角坐标系中,二次函数图象的顶点坐标为(4,- ),且在X轴上截得的线段AB长为6,请在Y轴上求一点P,(不写作法)使PA+PB的值最小,并求P点坐标。[轴对称法,2
),且在X轴上截得的线段AB长为6,请在Y轴上求一点P,(不写作法)使PA+PB的值最小,并求P点坐标。[轴对称法,2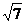 ]
]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com