1.下图所示的几何体的主视图是(　　 )

　　　　　　　　　　　　 A.　　　　　　 B.　　　　　 C.　　　 D.

2004、12、3

46、已知x+y+z=1,且0≤x≤1,0≤y≤1,2y+z≥,求M=2x+5y+4z的最大值和最小值。

　　　 [由x+y+z=1,z=1-x-y,M=-2x+y+4,y=2x+M-4；又由0≤x≤1，0≤y≤1，y≥x+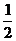，得x、y只能在如图(7)所示的阴影区域内变化，而M－4为直线在y轴上截距，随着M的变动，形成了一系列平行直线，M-4在0到1之间变化，所以4≤M≤5，M的最小值是4，最大值是5。]

　　　　　　　　　　　　　　　　　　　　 西塘中学　 杨孝华

45、设正整数a、b、c、d满足条件a/b=b/c=c/d=5/8,则a+b+c+d的最小值是________。

　　　　 [因为a=5/8·b,所以8∣b；同理d=8/5·c=64/25·b,25∣b；所以200∣b,当b=200时,a+b+c+d=1157是最小值。]

44、已知x,y,z为自然数，且x<y,x+y=1999,z-x=2000,求x+y+z的最大值。

　　　 [先用x替换y、z，得x+y+z=x+3999,当x最大时，x+y+z的值也最大，由1999-x≥1(y是自然数),1999-x>x(已知y>x),2000+x≥1(z是自然数)，所以1≤x<999_·5,所以x=999， x+y+z的最大值是4998。]

43、一个正整数除以5、7、9、11的余数依次为1、2、3、4，求满足上述条件的最小正整数。

　　　 [设这个数为P，则P-1能是5的倍数，P-2是7的倍数，P-3是9的倍数，P-4是11的倍数，且5、7、9、11、互质，5、7、9、11的最小公倍数是1731，]

42、求能使n³+100被n+10整除的最大整数n的值。

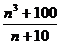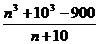　　　 [== n²-10n+100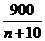－,n的最大值为890。]

41、设a、b、c是互不相同的自然数，ab²c³=1350，则a+b+c的最大值是_______。[ 1350=2×3³×5²=(2×3³)×5²×1³=(2×5²)×1²×3³=(2×3×5²)×3²×1³，所以有四解。]

40、代数式rvz-rwy-suz+swx+tuy-tvx中，r、s、t、u、v、w、x、y、z可以取1或者-1。(1)证明代数式的值为偶数；(2)求这个代数式所能取到的最大值。

　　　 [ 1中六项的值均为1或-1，且个数同奇同偶，所以和必为偶数；2六式相乘积为-(rstuvwxyz)²=-1,所以这六项中至少有一项为-1，这六项的和最多是5-1=4，取u、x、y为-1，其它字母为1，原式的最大值为4.]

39、将形状为等腰三角形的铁片改制成有一个内角为45⁰的平行四边形，问怎样做才能使材料的利用率最高？(接缝处材料损失不计)

　　　 [取AC、BC中点D、E，连结DE，把ΔCDE绕点E逆时针旋转180⁰，得ΔEBF，则ΔEBF≌ΔECD，这时四边形ADFB是平行四边形。它的面积就等于ΔABC的面积，材料利用率最高。]