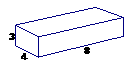
24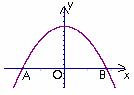．(本小题满分12分)有一座抛物线型拱桥，其水面宽为18米，拱顶离水面AB的距离为9米．有一货船要将打包好的一些长方体物品(长、宽、高分别是4米、3米、8米)放在甲板上运过拱桥(假设载货后船的甲板与水面大致平齐)．

(1)求抛物线的解析式．

(2)若货物堆放方式的正视图如下，问船能载货物通过拱桥吗？通过计算说明你的结论．

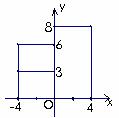
(3)若改变货物的堆放方式(正视图如下图甲、图乙)．问图甲和图乙能否载货物通过拱桥？假设此货船的甲板只能提供宽13米，长18米的置物空间，为了尽可能地多装这些长方体物品(略去其它因素)，你会选用图甲和图乙中的哪一种载物方式，为什么？

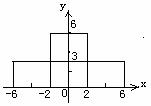
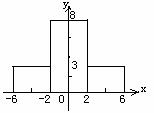
图甲　　　　　　　　　　　　　　　　　 图乙

23．(本小题满分10分)

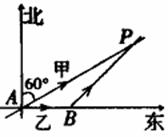
如图，甲、乙两辆货车于某日下午2:00同时从A地出发驶往P市，甲车沿一条公路向北偏东60°方向行驶，直达P市，其速度为30公里/小时；乙车先沿一条公路向正东方向行驶半小时后到达B地，卸下部分货物，再沿一条通向东北方向的公路驶往P市，其速度始终为40公里/小时．

(1)设出发后经过t小时，甲车与P市的距离为s，求s与t之间的函数关系式，并写出自变量t的取值范围；

(2)已知在P市新建的移动通讯接收发射塔，其信号覆盖面积可达P市周围方圆30公里的区域(包括边缘地带)，除此之外，该地区无其他发射塔，故甲、乙两车司机只能靠P市发射塔进行手机通话联系，问甲、乙两车司机从什么时刻开始可用手机取得联系(精确到分钟)？

说明：手机联系必须是两人都在信号覆盖范围内方可进行，否则，手机无法联系．

22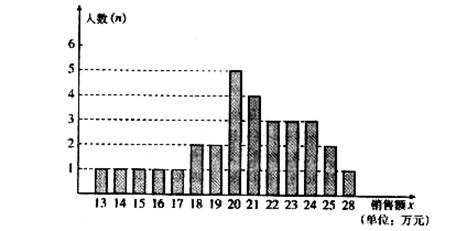．(本小题满分10分)某商场统计了每个营业员在某月的销售额，统计图如下：

解答下列问题：

(1)设营业员的月销售额为(单位：万元)，商场规定：当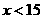时为不称职，当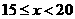时，为基本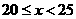称职，当为称职，当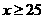时为优秀．试求出不称职、基本称职、称职、优秀四个层次营业员人数所占百分比(精确到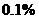)，并用扇形图统计出来．

(2)根据(1)中规定，所有称职和优秀这两个层次的营业员月销售额的中位数、众数和平均数分别是多少？

(3)为了调动营业员的工作积极性，决定制定月销售额奖励标准，凡到达或超过这个标准的营业员将受到奖励．如果要使得称职和优秀这两个层次的所有营业员的半数左右能获奖，你认为这个奖励标准应定为多少元合适？并简述其理由．

21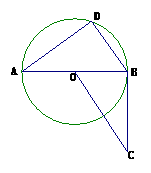．(本小题满分8分)如图，AB是⊙O的直径，BC是⊙O的切线，D是⊙O上的一点，且BD//CO．

(1)求证：△ADB∽△CBO；

(2)若AB=2，BC=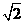，求AD的长(结果保留根号)．

20．(本小题满分8分) 如图，某工厂与A，B两地有公路、铁路相连．这家工厂从A地

购买一批每吨1000元的原料运回工厂，制成每吨8000元的产品运到B地．公路运价为

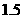元/(吨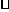千米)，铁路运价为元/(吨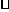千米)，这两次运输共支出公路运费15000元，铁路运费97200元．这批产品的销售款比原料费与运输费的和多多少元？

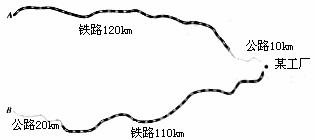
图中黑白相间的线表示铁路，其它线表示公路．　

19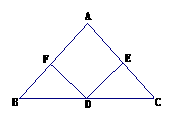．(本小题满分6分)已知：如图，D是△ABC的BC边的中点，DE⊥AC，DF⊥AB，垂足分别是E、F，且BF=CE．

求证：(1)△ABC是等腰三角形；

(2)当∠A=90°时，试判断四边形AFDE是怎样的四边形，

并证明你的结论．

18．(本小题满分6分)如图，在△ABC中，(1)用直尺和圆规作∠C的平分线CD交AB于D(保留作图痕迹，写出作法)；(2)若CD平分∠ACB，且∠A=70°，∠B=50°，求∠ACD

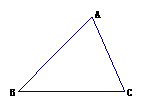的度数．

17．(本小题满分6分)

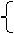解不等式组：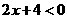　　　

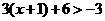
16.如图所示是在竖直平面内的一个“通道游戏”．图中竖直线段和斜线段都表示通道，并且在交点处相遇，若竖直线段有一条的为第一层，有二条的为第二层，依次类推，现有一颗小弹子从第一层的通道里向下运动．并且小弹子落入每一条通道的可能性相同，则该小弹子从第三层通道的出口B脱出的概率为　　　　　　　 ．

15.如图，在⊙O中，P是弦AB的中点，CD是过点P的直径，有下列五个结论：

①AB⊥CD；②∠AOB＝4∠ACD；③；④PO＝PD；⑤．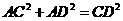

请把正确的结论序号填在横线上　　　　　　　 　；