
题目列表(包括答案和解析)
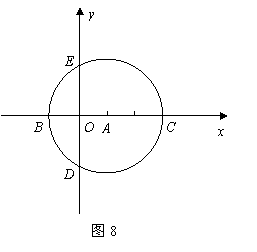
25.如图8,在直角坐标系中,以点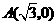 为圆心,以
为圆心,以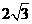 为半径的圆与
为半径的圆与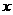 轴相交于点
轴相交于点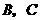 ,与
,与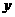 轴相交于点
轴相交于点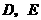 .
.
(1)若抛物线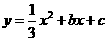 经过
经过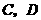 两点,求抛物线的解析式,并判断点
两点,求抛物线的解析式,并判断点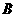 是否在该抛物线上.(6分)
是否在该抛物线上.(6分)
(2)在(1)中的抛物线的对称轴上求一点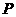 ,使得
,使得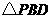 的周长最小.(3分)
的周长最小.(3分)
(3)设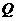 为(1)中的抛物线的对称轴上的一点,在抛物线上是否存在这样的点
为(1)中的抛物线的对称轴上的一点,在抛物线上是否存在这样的点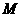 ,使得四边形
,使得四边形 是平行四边形.若存在,求出点
是平行四边形.若存在,求出点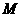 的坐标;若不存在,说明理由.(4分)
的坐标;若不存在,说明理由.(4分)
24.某电器经营业主计划购进一批同种型号的挂式空调和电风扇,若购进8台空调和20台电风扇,需要资金17400元,若购进10台空调和30台电风扇,需要资金22500元.
(1)求挂式空调和电风扇每台的采购价各是多少元?(5分)
(2)该经营业主计划购进这两种电器共70台,而可用于购买这两种电器的资金不超过30000元,根据市场行情,销售一台这样的空调可获利200元,销售一台这样的电风扇可获利30元.该业主希望当这两种电器销售完时,所获得的利润不少于3500元.试问该经营业主有哪几种进货方案?哪种方案获利最大?最大利润是多少?(5分)
23.在今年“五一”长假期间,某学校团委会要求学生参加一项社会调查活动.八年级学生小青想了解她所居住的小区500户居民的家庭收入情况,从中随机调查了40户居民家庭的收入情况(收入取整数,单位:元)并绘制了如下的频数分布表和频数分布直方图.
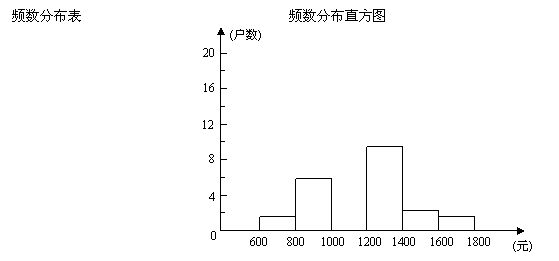
|
分组 |
频数 |
频率 |
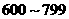 |
2 |
0.050 |
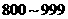 |
6 |
0.150 |
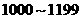 |
|
0.450 |
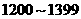 |
9 |
0.225 |
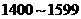 |
|
|
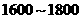 |
2 |
0.050 |
|
合计 |
40 |
1.000 |
根据以上提供的信息,解答下列问题:
(1) 补全频数分布表:(3分)
(2) 补全频数分布直方图;(2分)
(3) 这40户家庭收入的中位数落在哪一个小组?(2分)
(4) 请你估计该居民小区家庭收入较低(不足1000元)的户数大约有多少户?(3分)
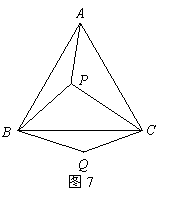
22.如图7,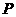 是等边三角形
是等边三角形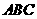 内的一点,连结
内的一点,连结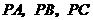 ,以
,以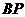 为边作
为边作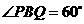 ,且
,且 ,连结
,连结 .
.
(1)观察并猜想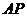 与
与 之间的大小关系,并证明你的结论.(4分)
之间的大小关系,并证明你的结论.(4分)
(2)若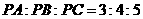 ,连结
,连结 ,试判断
,试判断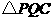 的形状,并说明理由.(4分)
的形状,并说明理由.(4分)
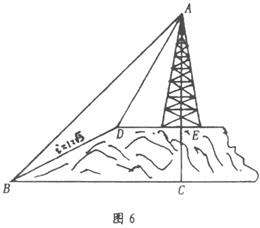
21.如图6,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度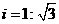 ,斜坡
,斜坡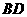 的长是50米,在山坡的坡底
的长是50米,在山坡的坡底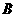 处测得铁架顶端
处测得铁架顶端 的仰角为
的仰角为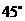 ,在山坡的坡顶
,在山坡的坡顶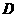 处测得铁架顶端
处测得铁架顶端 的仰角为
的仰角为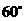 .
.
(1)求小山的高度;(4分)
 (2)求铁架的高度.(
(2)求铁架的高度.(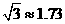 ,精确到0.1米)(4分)
,精确到0.1米)(4分)
20.如图5,已知反比例函数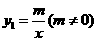 的图象经过点
的图象经过点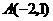 ,一次函数
,一次函数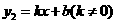 的图象经过点
的图象经过点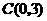 与点
与点 ,且与反比例函数的图象相交于另一点
,且与反比例函数的图象相交于另一点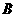 .
.
 (1)分别求出反比例函数与一次函数的解析式;(4分)
(1)分别求出反比例函数与一次函数的解析式;(4分)
(2)求点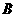 的坐标.(2分)
的坐标.(2分)
19.有2个信封,每个信封内各装有四张卡片,其中一个信封内的四张卡片上分别写有1、2、3、4四个数,另一个信封内的四张卡片分别写有5、6、7、8四个数,甲、乙两人商定了一个游戏,规则是:从这两个信封中各随机抽取一张卡片,然后把卡片上的两个数相乘,如果得到的积大于20,则甲获胜,否则乙获胜.
(1)请你通过列表(或画树状图)计算甲获胜的概率.(4分)
(2)你认为这个游戏公平吗?为什么?(2分)
18.先化简代数式: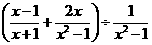 ,然后选取一个使原式有意义的
,然后选取一个使原式有意义的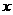 的值代入求值.
的值代入求值.
17.计算: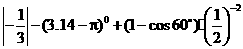
16.若用(1),(2),(3),(4)四幅图象分别表示变量之间的关系,将下面的(a),(b),(c),(d)对应的图象排序:

(a)面积为定值的矩形(矩形的相邻两边长的关系)
(b)运动员推出去的铅球(铅球的高度与时间的关系)
(c)一个弹簧不挂重物到逐渐挂重物(弹簧长度与所挂重物质量的关系)
(d)某人从 地到
地到 地后,停留一段时间,然后按原速返回(离开
地后,停留一段时间,然后按原速返回(离开 地的距离与时间的关系),其中正确的顺序是( )
地的距离与时间的关系),其中正确的顺序是( )
A.(3)(4)(1)(2) B.(3)(2)(1)(4)
C.(4)(3)(1)(2) D.(3)(4)(2)(1)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com