
题目列表(包括答案和解析)
3、二次函数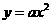 的图象过点(-1,2),则它的解析式是
,
的图象过点(-1,2),则它的解析式是
,
当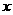 时,
时,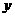 随
随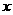 的增大而增大.
的增大而增大.
2、抛物线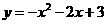 与
与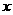 轴交点为 ,与
轴交点为 ,与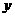 轴交点为 .
轴交点为 .
1、函数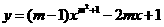 是抛物线,则
是抛物线,则 = .
= .
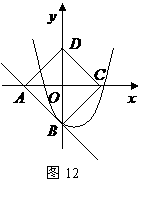 如图12,以边长为
如图12,以边长为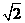 的正方形
的正方形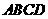 的对角线所在直线建立平面直角坐标系,抛物线
的对角线所在直线建立平面直角坐标系,抛物线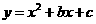 经过点
经过点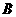 且与直线
且与直线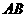 只有一个公共点.
只有一个公共点.
(1)求直线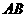 的解析式.(3分)
的解析式.(3分)
(2)求抛物线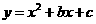 的解析式.(3分)
的解析式.(3分)
(3)若点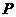 为(2)中抛物线上一点,过点
为(2)中抛物线上一点,过点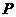 作
作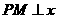 轴于点
轴于点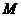 ,问是否存在这样的点
,问是否存在这样的点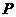 ,使
,使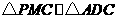 ?若存在,求出点
?若存在,求出点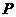 的坐标;若不存在,请说明理由.(5分)
的坐标;若不存在,请说明理由.(5分)
29.在学习勾股定理时,我们学会运用图(I)验证它的正确性;图中大正方形的面积可表示为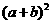 ,也可表示为
,也可表示为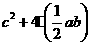 ,即
,即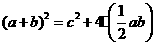 由此推出勾股定理
由此推出勾股定理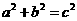 ,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
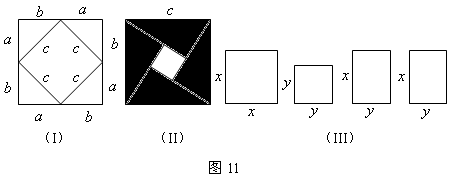
(1)请你用图(II)(2002年国际数字家大会会标)的面积表达式验证勾股定理(其中四个直角三角形全等).(3分)
(2)请你用(III)提供的图形进行组合,用组合图形的面积表达式验证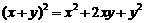 (3分)
(3分)
(3)请你自己设计图形的组合,用其面积表达式验证:
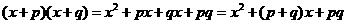 (4分).
(4分).
28.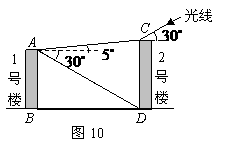 如图10所示,某学校拟建两幢平行的教学楼,现设计两楼相距30米,从
如图10所示,某学校拟建两幢平行的教学楼,现设计两楼相距30米,从 点看
点看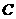 点,仰角为
点,仰角为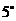 ;从
;从 点看
点看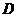 点,俯角为
点,俯角为 ,解决下列问题:
,解决下列问题:
(1)求两幢楼分别高多少米?(结果精确到1米)(6分)
(2)若冬日上午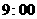 太阳光的入射角最低为
太阳光的入射角最低为 (光线与水平线的夹角),问一号楼的光照是否会有影响?请说明理由,若有,则两楼间距离应至少相距多少米时才会消除这种影响?(结果精确到1米)(4分)
(光线与水平线的夹角),问一号楼的光照是否会有影响?请说明理由,若有,则两楼间距离应至少相距多少米时才会消除这种影响?(结果精确到1米)(4分)
(参考数据: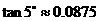
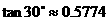
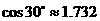 )
)
27.赵明暑假到光雾山旅游,从地理课上知道山区气温会随着海拔高度的增加而下降,沿途他利用随身所带的登山表,测得以下数据:
海拔高度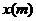 |
 |
 |
 |
 |
 |
气温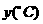 |
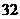 |
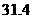 |
 |
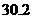 |
 |
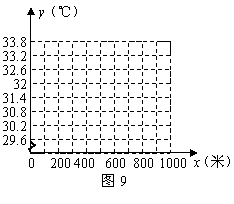
(1)现以海拔高度为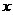 轴,气温为
轴,气温为 轴建立平面直角坐标系(如图9),根据上表中提供的数据描出各点.(3分)
轴建立平面直角坐标系(如图9),根据上表中提供的数据描出各点.(3分)
(2)已知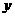 与
与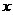 之间是一次函数关系,求出这个关系式.(5分)
之间是一次函数关系,求出这个关系式.(5分)
 (3)若赵明到达光雾山山巅时,测得当时气温为
(3)若赵明到达光雾山山巅时,测得当时气温为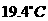 ,请求出这里的海拔高度.(2分)
,请求出这里的海拔高度.(2分)
26.巴中市进行课程改革已经五年了,为了了解学生对数学实验教材的喜欢程度,现对某中学初中学生进行了一次问卷调查,具体情况如下:

|
喜欢程序 |
非常喜欢 |
喜欢 |
不喜欢 |
|
人数 |
 人 人 |
|
 人 人 |
①已知该校初一共月480人,求该校初中学生总数.(2分)
②求该校初二学生人数及其扇形的圆心角度数.(3分)
③请补全统计表,并制作条形统计图来反映统计表中的内容.(5分)
④请计算不喜欢此教材的学生的频率,并对不喜欢此教材的同学提出一条建议,希望能通过你的建议让他喜欢上此教材.(2分)
25.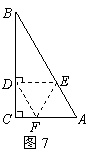 如图7,在
如图7,在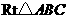 中,
中,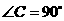 ,
,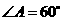 ,点
,点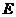 ,
,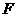 分别在
分别在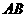 ,
, 上,把
上,把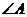 沿着
沿着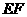 对折,使点
对折,使点 落在
落在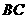 上点
上点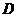 处,且使
处,且使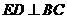 .
.
(1)猜测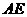 与
与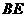 的数量关系,并说明理由.(5分)
的数量关系,并说明理由.(5分)
(2)求证:四边形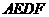 是菱形(5分)
是菱形(5分)
24.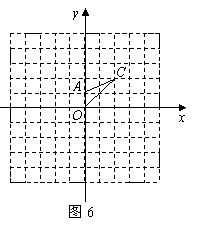 如图6,将
如图6,将 各顶点的横纵坐标分别乘以
各顶点的横纵坐标分别乘以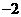 作为对应顶点的横纵坐标,得到所得的
作为对应顶点的横纵坐标,得到所得的 .
.
①在图中画出所得的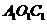 (4分)
(4分)
②猜想 与
与 的关系,并说明理由(5分)
的关系,并说明理由(5分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com