24.(本题满分11分)

便民超市准备将12 000元现金全部用于从某鱼面长以出厂价购进甲、乙两种不同包装的孝感特产云梦鱼面，然后以零售价对外销售.已知这两种鱼面的出厂价(元/盒)与零售价(元/盒)如下表：

⑴若超市购进甲种鱼面200盒，需付现金___________元，还剩余现金___________元，剩余的现金可购买乙种鱼面_____________盒；

⑵设超市购进的甲种鱼面为x(盒)，全部售出甲、乙两种鱼面所获的销售利润为y(元)，求y与x之间的函数关系式；

⑶在⑵的条件下，若甲、乙两种鱼面在保质期内的销售量都不超过500盒，求x的取值范围；并说明超市应怎样进货时获利最大？最大利润是多少？

23.(本题满分10分)

几何课本第三册复习题七中有这样一道几何题：以Rt△ABC的直角边AC为直径作圆，交斜边AB于点D，过点D作圆的切线.求证：这条切线平分另一条直角边BC.(不必证明)

现将上述习题改变成如下问题，请你解答：

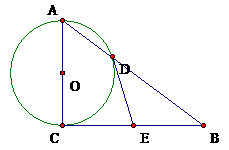
如图15，以Rt△ABC的直角边AC为直径作⊙O，交斜边AB于点D，E为BC边的中点，连DE.

⑴请判断DE是否为⊙O的切线，并证明你的结论.

⑵当AD：DB=9：16时，DE=8cm时，求⊙O的半径R.

22.(本题满分10分)

已知关于x的方程x²+(2k－1)x+(k－2)(k+1)……①和kx²+2(k－2)x+k－3……②.

⑴求证：方程①总有两个不相等的实数根；

⑵已知方程②有两个不相等的实数根，求实数k的取值范围；

⑶如果方程②的两个不相等实数根α、β的倒数和等于方程①的一个根，求k的值.

21.(本题满分9分)

为了解教学情况，某校抽取了部分初三年级学生期末数学考试成绩，将所得分数整理后，画出频率分布直方图(分数取整数，满分120分)，如图14所示，图中从左到右各小组的小长方形面积之比是5：16：13：9：7，第一小组的频数为10.

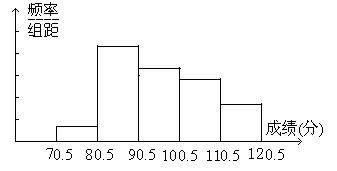
图14

请根据以上信息，回答下列问题：

⑴填空：第一小组的频率为_________；

⑵填空：在这个问题中，样本的容量是_____________；

⑶若分数在81分以上(含81分)为合格，试估计该校初三学生数学成绩的合格率是多少？(写出计算过程，并作答)

20.(本题满分8分)

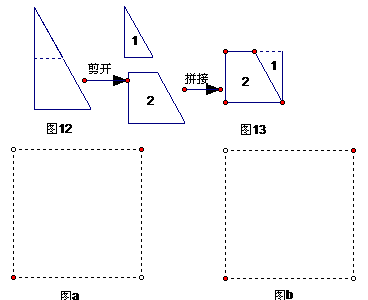
曙光中学在一次数学活动课上，学习几何图形的分割与拼接.首先，王老师将一直角三角形纸片从中位线处剪开成两部分，如图12所示，然后拼成图13所示的矩形纸片，现在请你利用王老师剪成的①、②两块纸片，再拼接成不同于图13的两个不同形状的四边形.

(不写画法，只需在图a、图b的虚线框内所拼图形的大致示意图)

19.(本题满分6分)

已知m=，先化简再求值：+.

18.为迎接2008年北京奥运会，孝感市某中学课外科技小组的同学们设计制作了一个电动智能玩具，玩具中的四个动物小鱼、小羊、燕子和熊猫分别在1、2、3、4号位置上(如图10)，玩具的程序是：让四个动物按图11所示的规律变换位置，第一次上、下两排交换位置；第二次是在第一次换位后，再左、右两列交换位置；第三次再上、下两排交换位置；第四次再左、右两列交换位置；按这种规律，一直交换下去，那么第2008次交换位置后，熊猫所在位置的号码是 _______________号.

17. 如图9，矩形ABCD沿DF折叠后，点C落在AB边上的点E处，DE、DF三等分∠ADC，若AB=6，则梯形ABFD的中位线的长为_______________.

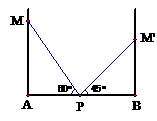
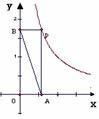
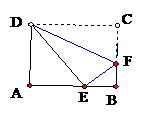
图7　　　　　　 图8　　　　　　　　 图9

16. 已知函数y=在第一象限的图象如图8所示，点P为图象上的任意一点，过P作PA⊥x轴于A，PB⊥y轴于B，则△APB的面积为_______________.

15. 如图7，在一间教室内有一个长为2a(a>0)米的梯子斜靠在墙上，梯子的倾斜角为60°.如果梯子底端不动，顶端靠在对面的墙上，此时梯子的倾斜角为45°，则这间教室的宽AB的长度为_______________米(结果不作近似计算).