2．下列四个图案中，符合右图所示的胶筒滚动后的图案是(　　 )

1.代数式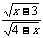有意义，则x的取值范围是(　　　 )

A．3<x<≤4　　　　　 B.3<x<4　　　 C.3≤x≤4　　 D.3≤x≤4

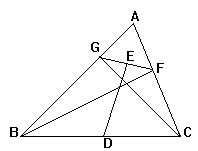
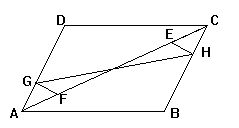
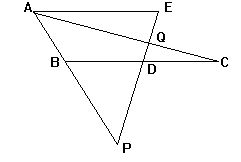
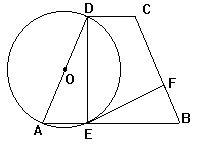
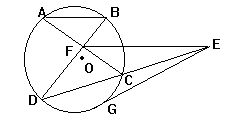
1.如图，在△ABC中，BF⊥AC,CG⊥AD,F、G是垂足，D、E分 　别是BC、FG的中点，求证：DE⊥FG 　 　 2.如图已知在平行四边形ABCD中，AF=CE，FG⊥AD于G， 　EH⊥BC于H，求证：GH与EF互相平分 　 3.如图，AE∥BC,D是BC的中点，ED交AC于Q，ED的延长线交 　AB的延长线于P，求证：PD·QE=PE·QD 　 　 4.如图，在梯形ABCD中，AB∥DC，AD=BC，以AD为直径的圆 　O交AB于点E，圆O的切线EF交BC于点F. 　求证：(1)∠DEF=∠B;(2)EF⊥BC 　　 　 5.如图，⊙O中弦AC，BD交于F，过F点作EF∥AB，交DC延 　长线于E，过E点作⊙O切线EG，G为切点，求证：EF=EG 　 　

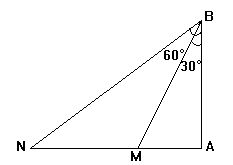
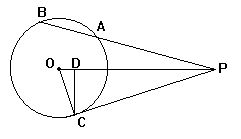
　第一次在B处望见该船在B的南偏西30°，半小时后，又望见该船 　在B的南偏西60°，求该船的速度． 　 2.已知⊙O的半径是2cm，PAB是⊙O的割线，PB=4cm,PA=3cm,PC 　是⊙O的切线，C是切点，CD⊥PO，垂足为D，求CD的长． 　 　 　

1.一个角的余角和它的补角互为补角，则这个角是 [ ] 　A.30°　 B.45°　 C.60°　 D.75° 　2.依次连结等腰梯形的各边中点所得的四边形是 [ ] 　A.矩形　 B.正方形 C.菱形　 D.梯形 　3.如图，DF∥EG∥BC,AD=DE=EB,△ABC被分成三部分的 　面积之比为 [ ] 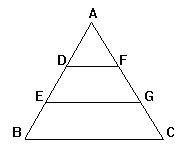　 　A.1∶2∶3　　 B.1∶1∶1 　C.1∶4∶9　　 D.1∶3∶5 　4.如果两个圆的半径分别为4cm和5cm,圆心距为1cm，那么这两个圆 　的位置关系是 [ ] 　A.相交　 B.内切　 C.外切　 D.外离 　5.已知扇形的圆心角为120°，半径为3cm,那么扇形的面积为[ ] 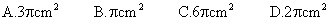　 　6.已知Rt△ABC的斜边为10，内切圆的半径为2，则两条直角边的 　长为 [ ] 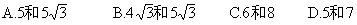　 　7.和距离为2cm的两条平行线都相切的圆的圆心的轨迹是 [ ] 　A.和两条平行线都平行的一条直线。 　B.在两条平行线之间且与两平行线都平行的一条直线。 　C.和两平行线的距离都等于2cm的一条平行线。 　D.和这两条平行线的距离都等于1cm的一条平行线。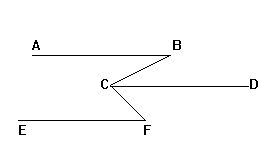 　8.过圆外一点作圆的割线PBC交圆于点B、C，作圆的切线PM，M 　为切点，若PB=2，BC=3，那么PM的长为 [ ] 　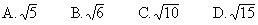 　9.已知：AB∥CD，EF∥CD,且∠ABC=20°，∠CFE=30°, 　则∠BCF的度数是 [ ] 　 　A.160° B.150° C.70° D.50° 　10.如图OA=OB，点C在OA上，点D在OB上，OC=OD，AD和 　BC相交于E，图中全等三角形共有 [ ] 　 　

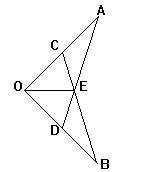
　A.2对　 B.3对　 C.4对　　 D.5对 　11.既是轴对称，又是中心对称的图形是 [ ] 　A.等腰三角形　　 B.等腰梯形 　C.平行四边形　　 D.线段 　 　

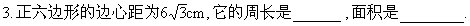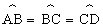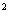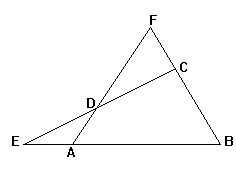
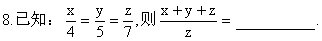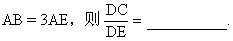
1.一个三角形的两条边长分别为9和2，第三边长为奇数，则第三边长为 . 2.△ABC三边长分别为3、4、5，与其相似的△A′B′C′的最大边长是 　10，则△A′B′C′的面积是 . 　 4.弦AC，BD在圆内相交于E，且，∠BEC=130°， 　则∠ACD= . 5.点O是平行四边形ABCD对角线的交点，若平行四边行ABCD的面 　积为8cm，则△AOB的面积为 . 6.直角三角形两直角边的长分别为5cm和12cm，则斜边上的中线长为 　 　　 . 7.梯形上底长为2，中位线长为5，则梯形的下底长为 . 　 9.如图，分别延长四边形ABCD两组对边交于E、F，若DF=2DA， 　 　 10.在Rt△ABC中，AD是斜边BC上的高，如果BC=a，∠B=30°， 　那么AD等于 . 　 　

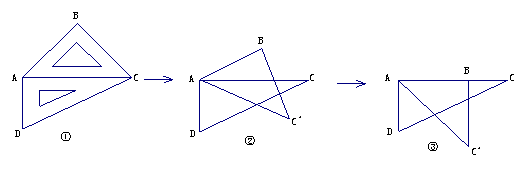
22.取一幅三角板按图①拼接，固定三角板ADC，将三角板ABC绕点A依顺时针方向旋转一个大小为α(0°＜α≤45°)得到△ABC＇，如图所示。

⑴当α为多少度时，能使得图②中AB∥CD？

⑵当旋转至图③位置，此时α又为多少度？图③中能找出几对相似三角形，并求其中一对的相似比；

⑶连结BD，当0°＜α≤45°探寻∠DBC＇+ ∠CAC＇ + ∠BDC大小变化状况，并证明。

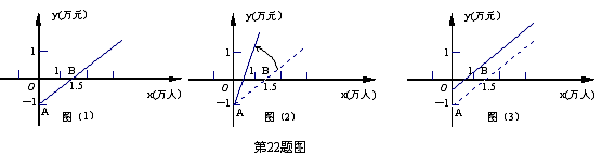
22、如图(1)是某公共汽车线路收支差额y(票价交流中心　收入减去运营成本)与乘客量x的函数图象。

目前这条线路亏损，为了扭亏，有关部门举行提高票价的听证会。

乘客代表认为：公交公司应节约能源，改善管理，降低运营成本，以此举实现扭亏。

公交公司认为：运营成本难以下降，公司已尽力，提高票价成本才能扭亏。

根据这两种意见，可以把图⑴分别改画成图⑵和图⑶。

⑴说明图⑴中点A和点B的实际意义。

⑵你认为图⑵和图⑶两个图象中，反映乘客意见的是_______，反映公交公司意见的是___________。

⑶如果公交公司采用适当提高票价又减少成本的办法实现扭亏为赢，请你在图⑷中画出符合这种办法的y与x的大致函数关系图象。

[解]

21. 某水果公司以2元/千克的成本新进了10000千克的柑橘，为了合理定出销售价格，水果公司在出售前要估算出在运输过程中可能损坏的水果总质量，以便将损坏的水果成本折算到没有损坏的水果售价中。销售人员首先从所有柑橘中随机地抽取若干柑橘，进行“柑橘损坏率”统计，获得的数据记录如下表(单位：千克)：

⑴上表“柑橘损坏率”一栏中的五个数据，众数是____；中位数是___；平均数_____。

⑵如果公司希望全部售完这些柑橘并获利润5000元，则出售这些柑橘时，每千克大约定价为多少元比较合适？(精确到0.1)

20.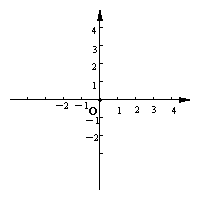某公司年初推出一种高科技产品，该产品销售的累积利润y(万元)与销售时间x(月)之间的关系(即前x个月的利润总和y与x之间的关系)为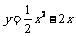(x>0)

⑴求出这函数的顶点坐标和对称轴；

⑵请在所给坐标系中，画出这个函数图象和简图；

⑶根据函数图象，你能否判断出公司的这种新产品销售累积利润是从什么时候开始盈利的？

⑷这个公司第6个月所获的利润是多少？