5、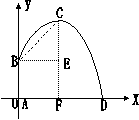改革开放后，不少农村用上了自动喷灌设备。如图所示，设

水管AB高出地面1.5米，在B处有一个自动旋转的喷水头，

一瞬间，喷出的水流呈抛物线状，喷头B与水流最高点C的

连线与水平地面成45⁰角，水流的最高点C比喷头B高出2米

，在所建的坐标系中，求水流的落地点D到A点的距离是多少米？

4、(1)一辆货车要通过跨度为8米，拱高为4米的单行抛物线隧道(从正中通过)，为保证安全，车顶离隧道顶部至少要0.5米的距离，求货车的限高应是多少？(精确到0.01米)

(2)若将(1)中的单行道改为双行道，即货车必须从隧道中线的右侧通过，求货车的限高应是多少？(如图)

3、今有网球从斜坡O点处抛出(如图)，网球的抛物线方程是

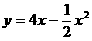，斜坡的方程是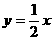，其中y是垂直高度(米)

x是与O点的水平距离(米)。

(1)　　　 网球落地时撞击斜坡的落点为A，写出A点的垂直高度，

以及A点与O点的水平距离。

(2)　　　 在图象中，标出网球所能达到的最高点B，并求出OB与水平线Ox之间夹角的正切。

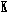
2、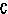某房地产公司要在一地块(图中矩形ABCD)上，规划建造一个小区公园(矩形GHCK)，为了使文物保护区△AEF不被破坏，矩形公园的顶点G不能在文物保护区内，已知AB＝200m，AD＝160m，AE＝60m，AF＝40m.

(1)　　 求矩形小区公园的顶点G恰是EF的中点时，公园的面积。

(2)　　 当G在EF上什么位置时，公园面积最大？

二次函数的应用

1、某商人如果将进货单价为8元的商品按每件10元出售，每天可销售100件。现在他采用提高售出价，减少进货量的办法增加利润，已知这种商品每涨价1元，其销售量就要减少10件，问他将售出价定为多少元时，才能使每天所赚利润最大？并求出最大利润。

例1、　　　　 某校校门是一抛物线形水泥建筑物，大门的地面宽度为8米，两侧距地面4米处各有一个挂校名横匾用的铁环，两铁环的水平距离为6米。

(1)　　　　 求校门的高是多少米？

(2)　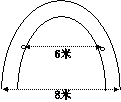　　　 由于学校性改善办学条件，有一高5米宽5米的大型工程车需进入校园，问该车能否顺利从校门通过？(水泥建筑物的厚度不计)

例2、　　　　 38岁的老乔丹第二次复出，表现依然神勇，在全场比赛还剩最后一秒时，奇才队仍以2分落后于纽约尼克斯队，在这关键时刻，乔丹在三分线外出手了!已知篮球的飞行路线是抛物线，乔丹的出手高度为2.37米，篮球在飞行了水平距离4米后，到达最高3.37米，问乔丹此次能否力挽狂澜(三分线是以篮框中心在地面的投影为圆心，6.25米为半径的半圆，篮框高度为3.05米)

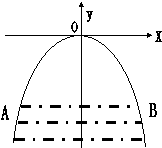
练习：某桥拱是抛物线形，它的截面如图所示，现测得水面宽AB＝8米，桥拱顶点O到水面的距离为4米，在图中直角坐标系内

(1)　　　　 求桥拱所在的抛物线的解析式；

(2)　　　　 某游船的水面以上部分高2米，宽6米，问该船能否顺利从桥下通过？

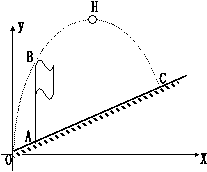
例3、　　　　 在斜坡A处立一旗杆AB(与水平面垂直)，一小球擦旗杆顶B而过，落地点为C，已知A点与O点的水平距离为1米，旗杆AB的高为3米，C点的垂直高度为3.5米，C点与O点的水平距离为7米，以O为原点，水平方向与竖直方向分别为x轴和y轴建立直角坐标系。

(1)　　　　 求小球经过的抛物线解析式；

(2)　　　　 H为小球所能到达的最高点，求OH与水平线Ox之间夹角的正切值。

(1)　　　 一般式：y＝ax²+bx+c　 (a≠0)　　 说明：(1)已知抛物线上任意三点，或不适　　　　　

(2)　　　 顶点式：y＝a(x+m)²+n　 (a≠0)　　　　　 合其他两种设法时，用一般式；　　

(3)　　　 交点式：y＝a(x－x₁)(x－x₂)　 (a≠0)　　 (2)已知抛物线顶点或能先求出抛物

　 线顶点时，用顶点式；

(3)已知抛物线与x轴两交点时，

用交点式(两根式)

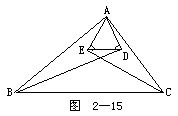
6．如图2-15所示．过△ABC的顶点A分别作两底角∠B和∠C的角平分线的垂线，AD⊥BD于D，AE⊥CE于E．求证：ED∥BC．

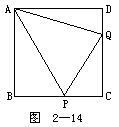
5．如图2-14所示．在正方形ABCD中，P，Q分别为BC，CD边上的点，∠PAQ=45。

求证：PQ=PB+DQ．

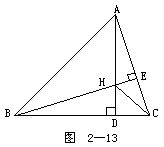
4．如图2-13所示．△ABC的高AD与BE相交于H，且BH=AC．

求证：∠BCH=∠ABC．