
题目列表(包括答案和解析)
1、 的值是
的值是
A.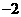 B.
B. C.
C.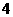 D.
D.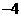
24、(本小题满分12分)
如图①,边长分别为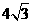 和3的两个等边三角形纸片ABC和
和3的两个等边三角形纸片ABC和 C′D′E′叠放在一起(C与C′重合)。
C′D′E′叠放在一起(C与C′重合)。
(1)
 操作:固定△ABC,将△C′D′E′绕点C顺时针旋转30°得到△CDE,连接AD、BE,CE的延长线交AB于F(如图②);
操作:固定△ABC,将△C′D′E′绕点C顺时针旋转30°得到△CDE,连接AD、BE,CE的延长线交AB于F(如图②);
探究:在图②中,线段BE与AD之间有怎样的大小关系?证明你的结论。
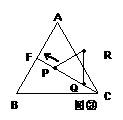 (2)
操作:如图②中的△C′DE沿着CF方向以每秒1个单位的速度平移,平移后的△C′DE设为△PQR(如图③);
(2)
操作:如图②中的△C′DE沿着CF方向以每秒1个单位的速度平移,平移后的△C′DE设为△PQR(如图③);
探究:设△PQR移动的时间为x 秒,△PQR与△AFC重叠部分的面积为y,求y与x之间的函数解析式,并写出自变量x的取值范围。

(3) 操作:将图①中的△C′D′E′固定,将△ABC移动,使顶点C落在C′E′的中点,边BC交D′E′于点M,边AC交D′C′于点N,设∠AC C′=α( 30°<α<90° )(如图④);
探究:在图④中,线段C′E×E′M的值是否随α的变化而变化?如果没有变化,求出C′E×E′M的值;如果有变化,说明理由。
23、 (本小题满分10分)
(本小题满分10分)
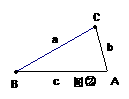
在△ABC中,∠A、∠B、∠C所对的边分别用a、b、c表示。
(1) 如图①,在△ABC中,∠A=2∠B,且∠A=60°。
求证: 。
。
(2)
如果一个三角形的一个内角等于另一个内角的2倍,我们就称这样的三角形为“倍角三角形”。本题图①中的三角形是特殊的倍角三角形,那么对于任意的倍角三角形(如图②),当∠A=2∠B时,关系式 是否仍然成立?若成立,证明你的结论;若不成立,举出反例。
是否仍然成立?若成立,证明你的结论;若不成立,举出反例。
(3) 是否存在这样的倍角三角形,其三边长恰为三个连续的正整数?若存在,求出其三边长;若不存在,说明理由。
22、(本小题满分10分)
某广告公司设计一幅周长为12米的矩形广告牌,广告设计费为每平方米100元。设矩形的一边长为x米,面积为S平方米。
(1) 求出S与x之间的函数关系式;
(2) 当x为多少米时,广告设计费最高?求出这个费用;
(3) 当x为多少米时,广告公司能获得500元的设计费?
(4) 当x的取值在什么范围内时,可使获得的广告设计费不低于500元?
21、(本小题满分8分)
 如图①,在矩形ABCD中,AD>AB,O为对角形的交点,过O作一直线MN分别交BC、AD于M、N。
如图①,在矩形ABCD中,AD>AB,O为对角形的交点,过O作一直线MN分别交BC、AD于M、N。
(1) 求证:梯形ABMN的面积等于梯形CDNM的面积;

(2) 如图②,将矩形ABCD以MN为轴对折,当MN满足什么条件时,对折后能使C点恰好与A点重合?(只写出需要满足的条件即可,不要求证明)
(3) 在(2)的条件下,判断四边形AMCN是什么特殊四边形?写出证明过程。
20、(本小题满分8分)
|
大蒜品种 |
甲 |
乙 |
丙 |
|
每辆汽车的满载量(吨) |
8 |
10 |
11 |
|
运输每吨大蒜获利(元) |
220 |
210 |
200 |
某运输公司计划用10辆汽车将甲、乙、丙三种大蒜共100吨运到外地,每辆汽车只能装同一种大蒜,且必须满载,每种大蒜不少于一车。
(1) 设用x辆车装甲种大蒜,y辆车装乙种大蒜,根据右表信息写出y与x之间的函数关系式,并说明有哪几种符合要求的运输方案。
(2)设此次运输的利润为P,求P与x之间的函数关系式,并说明按哪种方案运输利润最大。
19、(本小题满分6分)
如图,公路AB边有一人工湖,湖面上原有一座桥CD与公路垂直相通,因桥面有一部分断裂,为测桥长,站在完好的桥头D处测得路边的小树B在D的北偏西37.4°,前进50米到达E处,又测得小树B在E的北偏西45°。
(参考数据: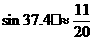 ;
; ;
; )
)
(1)
 计算桥CD的原有长度;
计算桥CD的原有长度;
(2) 若路边小树A与小树B相距50米,则小树A在点D的什么方向?
18、 (本小题满分6分)
(本小题满分6分)
某酒店为了吸引顾客,制做了一个可以自由转动的转盘,转盘等分成16份(如图),并规定:顾客每次消费200元以上(不包括200元),就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准八折、七折、五折区域,顾客就可以获得此项打折优惠。
(1) 如果一名顾客消费了300元,他获得打折优惠的概率是多少?
(2) 参加这个活动的顾客每转动一次转盘,平均可享受几折优惠?
17. (本小题满分6分)
(本小题满分6分)
饮食公司为某学校提供5元(A)、3元(B)和4元(C)三种价格的午餐供师生选择(每人限订一份),图①是5月份的销售情况统计图,这个月一共销售了10000份午餐。
(1) 写出师生购买午餐费用的中位数和众数。

(2) 如果5月份三种午餐的销售量与其平均每份的利润间的关系大致如图②所示,求该公司这个月在这所学校销售午餐共盈利多少元?

16.(本小题满分6分)
化简:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com