
题目列表(包括答案和解析)
29、 如图,ABCO是正方形,B(2,2),过D(-2,0)作直线
如图,ABCO是正方形,B(2,2),过D(-2,0)作直线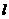 交OA于E,AB于F,若△DOE≌△FAE,求直线
交OA于E,AB于F,若△DOE≌△FAE,求直线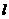 的解析式。若把正方形改为正三角形,即△AOB是正三角形,点B(2,0),过点C(-2,0)作直线
的解析式。若把正方形改为正三角形,即△AOB是正三角形,点B(2,0),过点C(-2,0)作直线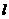 交AO于D,交AB于E,且使△ADE的面积和△DCO的面积相等,求直线
交AO于D,交AB于E,且使△ADE的面积和△DCO的面积相等,求直线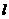 的解析式。(9分)
的解析式。(9分)
28、如图,在矩形ABCD中,对角线AC的长为10,且AB、BC(AB>BC)的长是关于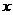 的方程
的方程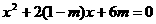 的两根。
的两根。
⑴求 的值;
的值;
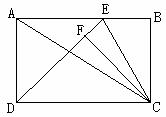 ⑵若E是AB上一点,CF⊥DE于F,求AE为何值时,△CEF的面积是△CED的面积的
⑵若E是AB上一点,CF⊥DE于F,求AE为何值时,△CEF的面积是△CED的面积的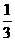 。(8分)
。(8分)
27、小明为书房买灯,现有两种灯可供选购,其中一种是9W(即0.009KW)的节能灯,售价为49元/盏;另一种是40W的白炽灯,售价为18元/盏。假设两种灯的照明亮度一样,使用寿命都可以达到2800小时,已知小明家所在地的电价为每KW0.5元。
⑴设照明时间为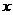 小时,请用含
小时,请用含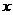 的代数式分别表示一盏节能灯和一盏白炽灯的费用。
的代数式分别表示一盏节能灯和一盏白炽灯的费用。
⑵小明想在这两种灯中选购一盏,问选哪一种灯合算?
⑶小明想在这两种灯中选两盏,假定照明时是3000小时,请你帮助他设计费用最低的选灯方案,并说明理由。(9分)
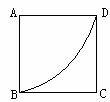
26、某个体生产厂想利用边长为8㎝的正方形做一批工艺品,设计方案如下:以A为圆心,8㎝长为半径裁扇形ABD,把扇形ABD卷成一个圆锥,正方形余下的部分裁出一个圆,问这个圆能否做上述卷成圆锥的底?若能,请计算出这个圆锥工艺品的高。若不能,请说明为什么?并帮这个生产厂提出一个改进的设计方案。(8分)

25、已知关于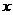 的方程
的方程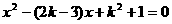 ,⑴当
,⑴当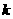 为何值时,此方程有实数根;⑵若此时方程的两实数根为
为何值时,此方程有实数根;⑵若此时方程的两实数根为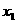 ,
,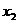 ,满足:
,满足: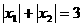 ,求
,求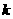 的值。(6分)
的值。(6分)
24、已知:如图,两个等圆⊙O1和⊙O2相交于A、B两点,过A作⊙O1的直径AC,与⊙O2交于点D,E为DC中点,
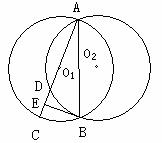 ⑴求证:AC⊥BE;⑵若两圆的半径都是5㎝,且AD∶DC=3∶2,求AB的长。(6分)
⑴求证:AC⊥BE;⑵若两圆的半径都是5㎝,且AD∶DC=3∶2,求AB的长。(6分)
23、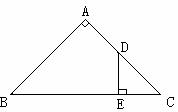 如图Rt△ABC中,∠A=90°,AB=AC,D是∠B的平分线与AC的交点,DE⊥BC于E。请猜想△DEC的周长与BC的关系?并证明你的猜想。(4分)
如图Rt△ABC中,∠A=90°,AB=AC,D是∠B的平分线与AC的交点,DE⊥BC于E。请猜想△DEC的周长与BC的关系?并证明你的猜想。(4分)
22、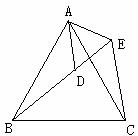 已知:如图△ABC和△ADE都是等边三角形,图中哪个三角形与△ABD全等?证明你的结论。(4分)
已知:如图△ABC和△ADE都是等边三角形,图中哪个三角形与△ABD全等?证明你的结论。(4分)
21、解方程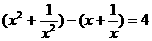 (4分)
(4分)
20、解方程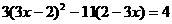 (4分)
(4分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com