
题目列表(包括答案和解析)
24.如图(1),在矩形ABCD中,AB=10cm,BC=8cm,点P从A点出发,沿A→B→C→D路线运动,到D停止;点Q从D出发,沿D→C→B→A路线运动,到A停止,若点P、点Q同时出发,点P的速度为1 cm/s,点Q的速度为2 cm/s,as后点P、点Q同时改变速度,点P的速度变为b cm/s,点Q的速度变为d cm/s。图(2)是点P出发x s后△APD的面积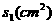
与 的函数关系图象;图(3)是点Q出发x s后△AQD的面积
的函数关系图象;图(3)是点Q出发x s后△AQD的面积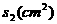 与
与 的函数关系图象。
的函数关系图象。

(1)参照图(2),求a、b及图(2)中c的值;
(2)求d的值;
(3)设点P离开点A的路程为 ,点Q到点A还需走的路程为
,点Q到点A还需走的路程为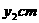 ,请分别写出动点P、Q改变速度后
,请分别写出动点P、Q改变速度后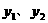 与出发后的运动时间
与出发后的运动时间 的函数关系式,并求出P、Q相遇时x的值;
的函数关系式,并求出P、Q相遇时x的值;
(4)当点Q出发__________秒时,点P、点Q在运动路线上相距的路程为25cm。
24. 如图,在矩形ABCD中,AB=10cm,BC=20cm.P、Q两点同时从A点出发,分别以1cm/秒和2cm/秒的速度沿A-B-C-D-A运动,当Q点回到A点时,P、Q两点即停止运动,设点P、Q运动时间为t秒。
(1) 当P、Q分别在AB边和BC边上运动时,设以P、B、Q为顶点的三角形面积为s,请写出s关于t的函数解析式及自变量t的取值范围。
(2) 在整个运动过程中,t取何值时,PQ与BD垂直。 A D

 (12分)
(12分)
B C
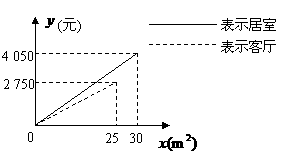
23.小亮家最近购买了一套住房.准备在装修时用木质地板铺设居室,用瓷砖铺设客厅.经市场调查得知:用这两种材料铺设地面的工钱不一样.小亮根据地面的面积,对铺设居室和客厅的费用(购买材料和工钱)分别做了预算,通过列表,并用 (m
(m )表示铺设地面的面积,用
)表示铺设地面的面积,用 (元)表示铺设费用,制成下图,请你根据图中所提供的信息,解答下列问题:
(元)表示铺设费用,制成下图,请你根据图中所提供的信息,解答下列问题:
(1)预算中铺设居室的费用为 元/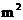 ,铺设客厅的费用为 元/
,铺设客厅的费用为 元/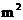 .
.
(2)表示铺设居室的费用 (元)与面积
(元)与面积 (
(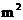 )之间的函数关系式为 .
)之间的函数关系式为 .
表示铺设客厅的费用 (元)与面积
(元)与面积 (
(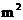 )之间的函数关系式为 .
)之间的函数关系式为 .
(3)已知小亮的预算中.铺设1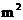 的瓷砖比铺设1
的瓷砖比铺设1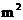 木质地板的工钱多5元;购买1
木质地板的工钱多5元;购买1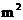 的瓷砖是购买1
的瓷砖是购买1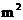 木质地板费用的
木质地板费用的 .那么,铺设每平方米木质地板、瓷砖的工钱各是多少?购买每平方米的木质地板、瓷砖的费用各是多少元?
.那么,铺设每平方米木质地板、瓷砖的工钱各是多少?购买每平方米的木质地板、瓷砖的费用各是多少元?
解:(1)135 110。…………………2分
(2)
 .…………………6分
.…………………6分
(3)设铺设每平方米木质地板的工钱是 元,购买每平方米木质地板的费用是
元,购买每平方米木质地板的费用是
元.根据题意得…………………7分
 …………………9分
…………………9分
解之得 …………………11分
…………………11分
 .…………………12分
.…………………12分
答:铺木质地板和瓷砖每平方米的工钱分别是15元和20元;购买木质地板
和瓷砖每平方米的费用为120元和90元. …………………13分
8.2÷0.25=32.8
∴课间10分钟最多有32人及时接完水.………………………………12分
或 设课间10分钟最多有z人及时接完水
由题意可得 0.25z≤8.2 z≤32.8
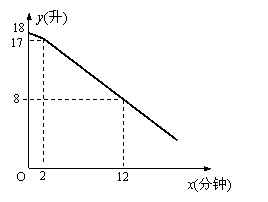
23. 教室里放有一台饮水机(如图),饮水机上有两个放水管.课间同学们依次到饮水机前用茶杯接水.假设接水过程中水不发生泼洒,每个同学所接的水量都是相等的.两个放水管同时打开时,他们的流量相同.放水时先打开一个水管,过一会儿,再打开第二个水管,放水过程中阀门一直开着.饮水机的存水量y(升)与放水时间x(分钟)的函数关系如图所示:
(1)求出饮水机的存水量y(升)与放水时间x(分钟)(x≥2)的函数关系式;(4分)
(2)如果打开第一个水管后,2分钟时恰好有4个同学接水结束,则前22个同学接水结束共需要几分钟?(4分)
(3)按(2)的放法,求出在课间10分钟内班级中最多有多少个同学能及时接完水?
 (4分)
(4分)
解(1)设存水量y与放水时间x的解析式为y=kx+b………………………1分
把(2,17)、(12,8)代入y=kx+b得
 解得k=-
解得k=-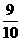 ,b=
,b=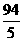 …………………………………3分
…………………………………3分
y=-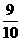 x+
x+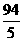 (2≤x≤
(2≤x≤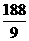 )………………………………………4分
)………………………………………4分
(2)由图可得每个同学接水量是0.25升………………………………………5分
则前22个同学需接水0.25×22=5.5升
存水量y=18-5.5=12.5升 ………………………………………………6分
∴12.5=-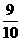 x+
x+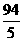 ∴x=7……………………………………………7分
∴x=7……………………………………………7分
∴前22个同学接水共需7分钟.
(3)当x=10时 存水量y=-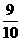 ×10+
×10+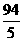 =
=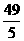 ……………………………9分
……………………………9分
用去水18-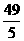 =8.2升………………………………………………………10分
=8.2升………………………………………………………10分
25、为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做了如下的探索:
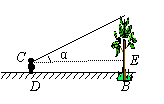
 实践一:根据《自然科学》中的反射定律,利用一面镜子和一根皮尺,设计如右示意图的测量方案:把镜子放在离树(AB)8.7米的点E处,然后沿着直线BE后退到点D,这是恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.6米,请你计算树(AB)的高度.(精确到0.1米)
实践一:根据《自然科学》中的反射定律,利用一面镜子和一根皮尺,设计如右示意图的测量方案:把镜子放在离树(AB)8.7米的点E处,然后沿着直线BE后退到点D,这是恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.6米,请你计算树(AB)的高度.(精确到0.1米)
 实践二:提供选用的测量工具有:①皮尺一根;②教学用三角板一副;③长为2.5米的标杆一根;④高度为1.5米的测角仪(能测量仰角、俯角的仪器)一架。请根据你所设计的测量方案,回答下列问题:
实践二:提供选用的测量工具有:①皮尺一根;②教学用三角板一副;③长为2.5米的标杆一根;④高度为1.5米的测角仪(能测量仰角、俯角的仪器)一架。请根据你所设计的测量方案,回答下列问题:
(1)在你设计的方案中,选用的测量工具是(用工
具的序号填写)
(2)在右图中画出你的测量方案示意图;
(3)你需要测得示意图中的哪些数据,并分别用a、b、c、α等表示测得的数据:
(4)写出求树高的算式:AB=
25解:实践一:由题意知 ∠CED=∠AEB,∠CDE=∠ABE=Rt∠
∴△CED∽△AEB 3分
∴ ∴
∴
∴AB≈5.2米 5分
 实践二:
实践二:
方案(一)(1)①② ;(6分)
(2)示意图如右;(7分)
(3)CD=a,BD=b;(8分)
|
 (注:取∠ACE=60°或30°时,则相应给分)
(注:取∠ACE=60°或30°时,则相应给分)
方案(二)(1)①④;(6分)
(2)示意图如右;(7分)
(3)BD=a,∠ACE=α;(8分)
(4)AB=a·tgα+1.5(10分)
 方案(三)(1)①③;(6分)
方案(三)(1)①③;(6分)
(2)示意图如右;(7分)
(3)CD=a,FD=b,DB=c;(8分)
(4)AB= (10分)
(10分)
(注:本题有其它测量方案,只要方法合理,则相应给分)
21. 一个长方形足球场的长为x m,宽为70m.如果它的周长大于350m,面积小于7560 ,求x的取植范围,并判断这个球场是否可以用作国际足球比赛.
(注:用于国际比赛的足球场的长在100m到110m之间,宽在64m到75m之间.)
,求x的取植范围,并判断这个球场是否可以用作国际足球比赛.
(注:用于国际比赛的足球场的长在100m到110m之间,宽在64m到75m之间.)
20. 现有一块形如母子正方形的板材,木工师傅想先把它分割成几块,然后适当拼接,制成某种特殊形状的板面(要求板材不能有剩余,拼接时不重叠、无空隙),请你按下列要求,帮助木工师傅分别设计一种方案:
(1) 板面形状为非正方形的中心对称图形;
(2) 板面形状为等腰梯形;
(3) 板面形状为正方形。
 请在方格纸中的图形上画出分割线,在相应的下边的方格纸上面拼接后的图形。
请在方格纸中的图形上画出分割线,在相应的下边的方格纸上面拼接后的图形。
19. 温州奥康集团对应聘者甲、乙、丙进行面试,并从专业知识、工作经验、仪表形象三方面给应聘者打分,每一方面满分20分,最后的打分制成条形统计图(如图).
(1)利用图中提供的信息,在专业知 识方面3人得分的极差是多少?在工作经验方面3人得分的众数是多少?在仪表形象方面谁最有优势?(3分)
(2)如果专业知识、工作经验、仪表形象三个方面的重要性之比为10∶7∶3,那么作为人事主管,你应该录用哪一位应聘者?为什么?(4分)
(3)在(2)的条件下,你对落聘者有何建议?(3分)
17.(1)计算:2cos60°+ (- )-1 -(-2) 2 .
)-1 -(-2) 2 .
(2)先化简: .再选一个你喜欢又合理的数求值.
.再选一个你喜欢又合理的数求值.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com