
题目列表(包括答案和解析)
27.如图1,已知 中,
中, ,
, ,过点
,过点 作
作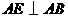 ,且
,且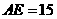 ,连接
,连接 交
交 于点
于点 .
.
(1)求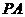 的长;
的长;
(2)以点 为圆心,
为圆心,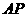 为半径作
为半径作 ,试判断
,试判断 与
与 是否相切,并说明理由;
是否相切,并说明理由;
(3)如图2,过点 作
作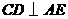 ,垂足为
,垂足为 .以点
.以点 为圆心,
为圆心, 为半径作
为半径作 ;以点
;以点 为圆心,
为圆心, 为半径作
为半径作 .若
.若 和
和 的大小是可变化的,并且在变化过程中保持
的大小是可变化的,并且在变化过程中保持 和
和 相切,且使
相切,且使 点在
点在 的内部,
的内部, 点在
点在 的外部,求
的外部,求 和
和 的变化范围.
的变化范围.

26.(本题8分)如图1,以矩形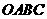 的两边
的两边 和
和 所在的直线为
所在的直线为 轴、
轴、 轴建立平面直角坐标系,
轴建立平面直角坐标系, 点的坐标为
点的坐标为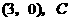 点的坐标为
点的坐标为 .将矩形
.将矩形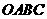 绕
绕 点逆时针旋转,使
点逆时针旋转,使 点落在
点落在 轴的正半轴上,旋转后的矩形为
轴的正半轴上,旋转后的矩形为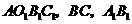 相交于点
相交于点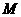 .
.
(1)求点 的坐标与线段
的坐标与线段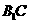 的长;
的长;
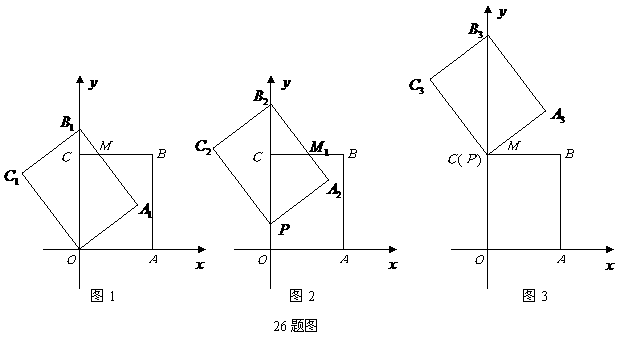
(2)将图1中的矩形 沿
沿 轴向上平移,如图2,矩形
轴向上平移,如图2,矩形 是平移过程中的某一位置,
是平移过程中的某一位置, 相交于点
相交于点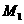 ,点
,点 运动到
运动到 点停止.设点
点停止.设点 运动的距离为
运动的距离为 ,矩形
,矩形 与原矩形
与原矩形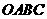 重叠部分的面积为
重叠部分的面积为 ,求
,求 关于
关于 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;
 (3)如图3,当点
(3)如图3,当点 运动到点
运动到点 时,平移后的矩形为
时,平移后的矩形为 .请你思考如何通过图形变换使矩形
.请你思考如何通过图形变换使矩形 与原矩形
与原矩形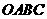 重合,请简述你的做法.
重合,请简述你的做法.
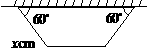
25.(本题7分)某校数学研究性学习小组准备设计一种高为60cm的简易废纸箱.如图1,废纸箱的一面利用墙,放置在地面上,利用地面作底,其它的面用一张边长为60cm的正方形硬纸板围成.经研究发现:由于废纸箱的高是确定的,所以废纸箱的横截面图形面积越大,则它的容积越大.
 (1)该小组通过多次尝试,最终选定下表中的简便且易操作的三种横截面图形,如图2,是根据这三种横截面图形的面积
(1)该小组通过多次尝试,最终选定下表中的简便且易操作的三种横截面图形,如图2,是根据这三种横截面图形的面积 与
与 (见表中横面图形所示)的函数关系式而绘制出的图象.请你根据有关信息在表中空白处填上适当的数、式,并完成
(见表中横面图形所示)的函数关系式而绘制出的图象.请你根据有关信息在表中空白处填上适当的数、式,并完成 取最大值时的设计示意图;
取最大值时的设计示意图;
|
横截面图形 |
|
 |
 |
 与 与 的函数关系式 的函数关系式 |
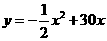 |
|
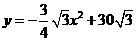 |
 取最大值时 取最大值时 (cm)的值 (cm)的值 |
30 |
|
20 |
 取得的最大值 取得的最大值 |
 450 450 |
|
 |
 取最大值时的设计示意图 取最大值时的设计示意图 |
|
 |
 |
 (2)在研究性学习小组展示研究成果时,小华同学指出:图2中“底角为
(2)在研究性学习小组展示研究成果时,小华同学指出:图2中“底角为 的等腰梯形”的图象与其他两个图象比较,还缺少一部分,应该补画.你认为他的说法确吗?请简要说明理由.
的等腰梯形”的图象与其他两个图象比较,还缺少一部分,应该补画.你认为他的说法确吗?请简要说明理由.
24.(本题7分)如图,在 与
与 中,
中, ,
,
 相交于点
相交于点 ,过点
,过点 作
作 交
交 的延长线于点
的延长线于点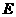 ,过点
,过点 作
作 交
交 的延长线于点
的延长线于点 相交于点
相交于点 .
.
(1)图中有若干对三角形是全等的,请你任选一对进行证明;(不添加任何辅助线)
(2)证明四边形 是菱形;
是菱形;
 (3)若使四边形
(3)若使四边形 是正方形,还需在
是正方形,还需在 的边长之间添加一个什么条件?请你写出这个条件.(不必证明)
的边长之间添加一个什么条件?请你写出这个条件.(不必证明)
23.(本题6分)某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对她所任教的初三(1)班和(2)班进行了检测.如图表示从两班各椭机抽取的10名学生的得分情况:
(1)利用图中提供的信息,补全下表:
|
班级 |
平均数(分) |
中位数(分) |
众数(分) |
|
(1)班 |
|
24 |
24 |
|
(2)班 |
24 |
|
|
(2)若把24分以上(含24分)记为“优秀”,两班各有60名学生,请估计两班各有多少名学生成绩优秀;
(3)观察图中的数据分布情况,你认为哪个班的学生纠错的整体情况更好一些?

22.(本题6分)如图1, 分别表示边长为
分别表示边长为 的等边三角形和正方形,
的等边三角形和正方形, 表示直径为
表示直径为 的圆.图2是选择基本图形
的圆.图2是选择基本图形 用尺规画出的图案,
用尺规画出的图案,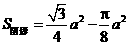 .
.
(1)请你从图1中任意选择两种基本图形,按给定图形的大小设计一个新图案,还要选择恰当的图形部分涂上阴影,并计算阴影的面积;(尺规作图,不写作法,保留痕迹,作直角时可以使用三角板)
 (2)请你写一句在完成本题的过程中感受较深且与数学有关的话.
(2)请你写一句在完成本题的过程中感受较深且与数学有关的话.
21.(本题6分)元旦联欢会前某班布置教室,同学们利用彩纸条粘成一环套一环的彩纸链,小颖测量了部分彩纸链的长度,她得到的数据如下表:
纸环数 (个) (个) |
1 |
2 |
3 |
4 |
…… |
彩纸链长度 (cm) (cm) |
19 |
36 |
53 |
70 |
…… |
(1)把上表中 的各组对应值作为点的坐标,在如图的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在如图的平面直角坐标系中描出相应的点,猜想 与
与 的函数关系,并求出函数关系式;
的函数关系,并求出函数关系式;
 (2)教室天花板对角线长10m,现需沿天花板对角线各拉一根彩纸链,则每根彩纸链至少用多少个纸环?
(2)教室天花板对角线长10m,现需沿天花板对角线各拉一根彩纸链,则每根彩纸链至少用多少个纸环?
20.(本题7分)某高校共有5个餐厅和2个小餐厅,经过测试:同时开放1个大餐厅、2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅、1个小餐厅,可供2280名学生就餐.
(1)求1个大餐厅、1个小餐厅分别可供多少名学生就餐;
(2)若7个大餐厅同时开放,能否供全校的5300名学生就餐?请说明理由.
19.(本题6分)小明和小丽用形状大小相同、面值不同的5张邮票设计了一个游戏,将面值1元、2元、3元的邮票各一张装入一个信封,面值4元、5元的邮票各一张装入另一个信封.游戏规定:分别从两个信封中各抽取1张邮票,若它们的面值和是偶数,则小明赢;若它们的面值和是奇数,则小丽赢,请你判断这个游戏对双方是否公平,并说明理由.
18.(本题5分)解方程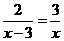 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com