29．已知:正方形ABCD的对角线AC、BD相交于点O，点P是直线AB上一点，PE⊥BD交直

线BD于点E，DF⊥AC交直线AC于点F,M是边AB的中点.

(1)如左图，当点P在边BC上时，①求证: PE+OE＝AO；②求证:ME=MF;

(2)如右图，当点P在线段AB的延长线上时，请你根据题意画出正确的图形，探求

结论: ME=MF是否成立, 并说明理由．

28．操作与探究：

(1)图①是一块直角三角形纸片。将该三角形纸片按如图方法折叠，使点A与点C重合，DE为折痕。试证明△CBE等腰三角形；

(2)再将图①中的△CBE沿对称轴EF折叠(如图②)。通过折叠，原三角形恰好折成两个重合的矩形，其中一个是内接矩形，另一个是拼合(指无缝无重叠)所成的矩形，我们称这样的两个矩形为“组合矩形”。你能将图③中的△ABC折叠成一个组合矩形吗？如果能折成，请在图③中画出折痕；

(3)请你在图④的方格纸中画出一个斜三角形，同时满足下列条件：①折成的组合矩形为正方形；②顶点都在格点(各小正方形的顶点)上；

(4)有一些特殊的四边形，如菱形，通过折叠也能折成组合矩形(其中的内接矩形的四个顶点分别在原四边形的四条边上)。请你进一步探究，一个非特殊的四边形(指除平行四边形、梯形外的四边形)，当满足条件　　　　　　　　　 时，一定能折成组合矩形？

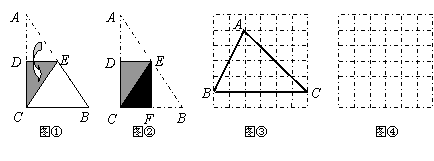
27．已知：如图，矩形ABCD中，AB=6cm，AD=8cm，动点F从A点出发，沿AD以4cm/s的速度运动；同时动点E从B点出发，沿对角线BD以5cm/s的速度运动，设运动的时间为ts(t<2).

(1)求证：四边形ABEF为梯形；

(2)当t为何值时，梯形ABEF的面积是△BDC面积的一半.

26．如图，在四边形ABCD中，AB=DC，E、F分别是AD、BC的中点，G、H分别是对角线BD、AC的中点.

(1)四边形EGFH是怎样的四边形？请证明你的结论；

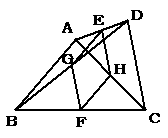(2)连接EF，探求EF与AB的大小关系为　　　　 (填“>”、“=”或“<”)，并证明你的结论.

25．操作与证明：用一张矩形纸片折等边三角形.

(1)如图①,把矩形纸片ABCD对折后再展开,折痕为EF;

图①　　　　　　　　　　　　　　　　　　 图②

(2)如图②, 将点A翻折到EF上的点A’处,且使折痕过点B;

(3)如图③,沿A’A折叠,得△A’BA.

△A’BA是等边三角形吗?请说明理由.

图③

23．已知:如图,平行四边形ABCD的对角线AC的平分线与边AD、BC分别相交于E 、F.

求证：四边形AFCE是平行四边形.　

22．如图, △ABC中, D、E分别是AC、AB上的点, BD与CE交于点O. 给出下列三个条件：①∠EBO=∠DCO；②∠BEO=∠CDO；③BE=CD.

⑴ 上述三个条件中,可判定△ABC是等腰三角形的两个条件为　　　　　　 (用序号写

出所有情形)；

⑵ 选择第⑴小题中的一种情形, 证明△ABC是等腰三角形.

21．已知:实数x、y满足y=,求的值.　

20．最简的二次根式与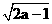是同类二次根式,求a的值.