3.如图(3)，一艘轮船从A处出发，以18节的速度向正北方向航行，经过10时到达B处，分别从A、B望灯塔C，测得∠NAC=42°，∠NBC=84°，则从B处到灯塔C的距离是　　　　 海里. (1节=1海里/小时)

2.如图(2)，在△ABC中，AB=AC，AB的垂直平分线交AC于点E，已知△BCE的周长为8，BC=3，则AB=　　　　 .

1.如图(1)，△ABC的外角∠CBD和∠BCE的平分线相交于点F，则点F一定还在

∠　　　　 的平分线上.

24.(8分)如图13－1，一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起．现正方形ABCD保持不动，将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转．

(1)如图13－2，当EF与AB相交于点M，GF与BD相交于点N时，通过观察或测量BM，FN的长度，猜想BM，FN满足的数量关系，并证明你的猜想；

(2)若三角尺GEF旋转到如图13－3所示的位置时，线段FE的延长线与AB的延长线相交于点M，线段BD的延长线与GF的延长线相交于点N，此时，(1)中的猜想还成立吗？若成立，请证明；若不成立，请说明理由．

附加题:(10分)如图，Rt_△ABO的顶点A是双曲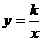线与直线在第二象限的交点，AB⊥轴于B且S_△ABO=

(1)求这两个函数的解析式。(2)求直线与双曲线的两个交点A，C的坐标。

(3)在x轴上是否存在点P，使△AOP为等腰三角形？

若存在，符合条件的点P有多少个，若不存在，请说明理由。

23．(6分)如图，A为双曲线上一点，过A作AC⊥x轴，垂足为C，且S_△AOC=2．

(1)　　 求该反比例函数解析式；

(2)　　 若点(-1,y₁),(-3,y₂)在双曲线上，试比较y₁、 y₂的大小．

22.(6分)某商店进了一批服装，进货单价为50元，如果按每件60元出售，可销售800件，如果每件提价1元出售，其销售量就减少20件。现在要获利12000元，且销售成本不超过24000元，问这种服装销售单价确定多少为宜？这时应进多少服装？

21.(6分)如图，在中，，点从点开始沿边向点以的速度匀速移动，同时另一点由点开始以的速度沿着匀速移动，几秒后，的面积等于？

20.(6分)求证：连接矩形各边中点得到的四边形为菱形。

19.(6分)如图4，正方形ABCD中，E为CD上一点，F为BC延长线上一点，CE=CF.

(1)求证：△BCE≌△DCF；(2)若∠BEC=60⁰，求∠EFD的度数.

18．(5分)已知，如图3，AB和DE是直立在地面上的两根立柱.AB=5m，某一时刻AB在阳光下的投影BC=3m.(1)请你在图3中画出此时DE在阳光下的投影；

(2)在测量AB的投影时，同时测量出DE在阳光下的投影长为6m，请你计算DE的长.