16.相切

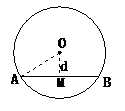解:如答图所示,连结OA,作OM⊥AB,垂足为M,则AM=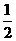AB,

∵AB= 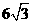, ∴AM=3 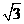,∵OA=6,

∴d=OM=　 ,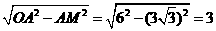

即d=OM=r=3,故以3为半径的同心圆与直径AB相切.

　　　 点拨: 在运用圆心到直线的距离与圆的半径大小来判断直线与圆的位置关系时,应避免认为“d”是圆心到直线上任一点的长.

15.44°

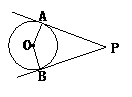解:如答图所示,∵PA、PB切⊙O于A、B,

∴∠OAP=∠OBP=90°,

∵∠AOB=136°四边形OAPB内角和为360°,

∴∠P=360°-∠OAP-∠OBP-∠AOB

=360°- 90°-90°-136°=44°.

　　　 点拨:见到圆的切线即得到该切线和过切点的半径垂直,这是一条很重要的结论.此题还应联想到使用四边形的有关知识.

14.

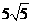
解:连结BM, ∵AM是直径,∴∠MBA=90°,∵AD⊥BC, ∴∠ADC=90°,

∴∠MBA=∠ADC=90°,又∵∠C=∠M,∴Rt△AMB∽Rt△ACD, ∴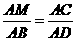

　∵AD=6,CD= 3,BD=8,

∴AB=,AC=

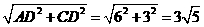
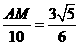　∴,∴AM=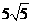

　　　 点拨:运用勾股定理及三角形相似解决该题,从而加强各知识点的沟通与综合运用.

13.6和4

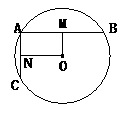解:如答图所示,∵AB⊥AC,OM⊥AB,ON⊥AC,

四边形OMAN是距形, 且AM=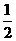AB,AN=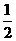AC,

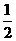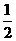∴OM=AN=2,ON=AM=3, 即AB=3, AC=2,

∴AB=6,AC=4.

　　　 点拨:运用垂径定理和矩形的有关性质来解决该题,从而避免读者构造直角三角形来解决的思路,读者难以依据题意正确地画图.

12.4

解:如答图所示,连结OA,过O作OM⊥AB,垂足为M,则AM=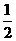AB,

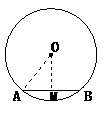∵AB=6cm,∴AM=3cm.∵⊙O直径为10cm,

∴OA=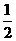×10=5(cm),

在Rt△OAM中,O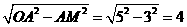M=(cm).

　　　 点拨:在解决与弦有关的问题时,常过圆心作弦的垂线段, 再利用垂径定理和勾股定理来解决.

11. 　

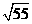
解:如答图所示,设AP切⊙O于P,连结OP,则OP⊥PA.在Rt△OPA中, OP=3,OA=OB+AB=3+5=8,∴PA=.

　　　 点拨:遇切线就连结切点和圆心得过切点的半径,这是一条常见的辅助线.

10.D

解:∵圆锥的母线长5cm,底面半径长3cm,圆锥的侧面展开图是扇形,

∴扇形的半径R=5cm,扇形的弧长L=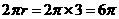(cm),

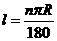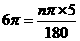∵,∴, ∴n=216°.

　　　 点拨:应正确区别圆柱与圆锥的侧面展开图,读者易将这两种立体图形的侧面积混淆.

9.B

解:∵R²+d²=r²+3Rd,∴(R²-2Rd+d²)-r²=0,∴(R-d)²-r²=0,∴(R-d+r)( R-d-r)=0,

∴R-d+r=0或R-d-r=0,∴d=R+r或d=R-r,∴两圆相外切或内切.

　　　 点拨:该题通过整理、分解因式得到d与R、r的关系, 即可判定两圆的位置关系,解答时易误得到一种情况,忽视另一种情况.

8.B

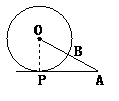
解:如答图所示,∵OA=AB,OA=OB,∴OA=OB=AB,

∴∠OBA=60°.∵BC 是⊙O的切线,

∴∠OBC=90°,∴∠ABC=∠OBA+OBC=60°+90°=150°.

∵BC=AB, ∴∠BAD=∠BCA=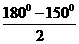=15°,

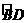∴的度数=30°.

∵∠OBC=90°,BC=OA=OB,∴△OBC 为等腰直角三角形,

∴∠BOE=45°,∴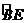的度数=45°,

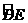∴的度数=(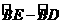)的度数=45°-30°=15°.

　　　 点拨:本题应用等边三角形、等腰三角形的知识解决了圆中弧的度数问题,解答量易将圆周角性质与圆心角性质混淆,应特别注意.

7.A

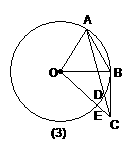
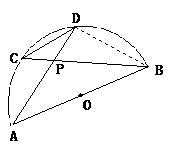解:如答图所示,连结BD,∵∠C=∠A,∠CPD=∠APB,

∴△CPD∽△APB,∴,

∵CD=3,AB=4,∴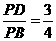,∴PD=3k,AB=4k,

∵AB是⊙O的直径,∴∠BDP=90°,

∴BD=,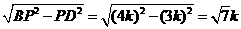

∴　 .

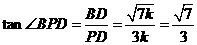点拨:该题是三角形相似、直径的性质以及解直角三角形的综合应用.在解直角三角形时,读者易由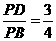,误认为PD=3、PB=4.