3、如图1，为了求出湖两岸A、B两点之间的距离，观测者测得DE=40m，且点D、E分别是线段AC、BC的中点，则A、B两点之间的距离为　　 _____m。

2、分解因式：4x²1＝________.

1、2005的相反数是____________。

28.一个圆形街心花园，有三个出口A、B、C，每个出口之间有一条长60米的道路，组成正三角形ABC，在中心点O处有一个亭子。为使亭子与原来的路相通，需修建三条小路OD、OE、OF，使另一出口D、E、F分别落在三角形ABC的三边上，且这三条路把三角形ABC分成三个全等的多边形，以备种植不同品种的花草。

(1)请你按以上要求设计两种不同的方案分别画在图1、图2上，并附简单说明；

(2)要使三条小路把三角形ABC分成三个全等的等腰梯形，应怎样设计？请把方案画在图3上，并求出此时三条小路的长度和；

(3)请你研究一种一般的方法，使得不论D在何处，都能准确的找出另外两个出口E、F的位置，请写出这个方法(图4供你探究用)

(4)你在图4中探究出的一般方法是否适用于正五边形？请结合图形进行说明。这种方法能推广到正n边形吗？

27.我市某地一家农工商公司收获的一种蔬菜，共140吨，若在市场上直接销售，每吨利润为1000元，经粗加工后销售，每吨利润可达4500元，经细加工后销售，每吨利润可达6500元。

该公司加工厂的能力是：如果对蔬菜进行粗加工，每天可加工16吨；如果进行细加工，每天可加工6吨，但两种加工方式不能同时进行，受季节等条件限制，公司必须在15天内(含15天)将这批蔬菜全部销售或加工完毕。为此，公司研制了两种方案：

　方案一。尽可能多的对蔬菜进行精加工，没来得及进行加工的蔬菜，在市场上直接销售。

　方案二。将一部分蔬菜进行精加工，其余蔬菜进行粗加工。

(1)求出方案一所获利润W₁。

(2)求出方案二所获利润W₂(元)与精加工蔬菜数X(吨)之间的函数关系式。

(3)你认为应如何安排加工(或直接销售)使公司获利最多？最大利润是多少

26．海棠牌”电热水器，每单位时间内进出水的水量都是一定的，设从某一时刻开始4分钟内只进冷水，不出热水，在随后的8分钟内既进冷水又出热水，如果时间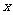(分)与水量(升)之间的函数关系如图所示．

　 (1)每分钟进水多少？

　 (2)当时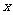，与y有何关系？

24．　 若方程(2m-1)x²-2x+1=0有两个不相等实数根。

(1)求m范围；　　　 (2)如果+=13, 求-值。

23．“学校校办厂需制作一块广告牌，请师徒两名工人，已知师傅单独做需4天，徒弟单独做需6天，现由徒弟先做一天，再由两人合作完成，

(1)　　　　 前后共用几天完成了任务？

(2)　　　　 如果完工后共得报酬450元，现按各人完成任务的工作量计算报酬，该如何分配？

22．有一块三角形的地，现要平均分四农户种植(即四等分三角形面积)，请你在图上作出分法。(不写作法，保留作图痕迹)