
题目列表(包括答案和解析)
1、下列方程:(1) (2)
(2)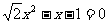 (3)
(3) (4)
(4)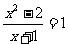 (5)
(5) 其中是一元二次方程的有(
);是分式方程的有(
)(填序号)
其中是一元二次方程的有(
);是分式方程的有(
)(填序号)
30、(本题12分)已知直线坐标系内有一条直线和一条曲线,这条直线和x轴负半轴、y轴正半轴分别交于点A、点B,且OA=OB=1,这条曲线是函数y=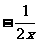 的图象在第二象限内一个分支,点P是这条曲线上任意一点,它的坐标是(a,b),由点P向x轴、y轴所作的垂线PM、PN(点M、N为垂足)分别与直线AB相交于点E、点F。
的图象在第二象限内一个分支,点P是这条曲线上任意一点,它的坐标是(a,b),由点P向x轴、y轴所作的垂线PM、PN(点M、N为垂足)分别与直线AB相交于点E、点F。
(1)设交点E和F都在线段AB上(如图所示),分别求点E、点F的坐标(用a的代数式表示点E的坐标,用b的代数式表示点F的坐标,只须写出答案,不要求写出计算过程);
(2)求△OEF的面积(结果用a、b的代数式表示);
(3)△AOF与△BEO是否一定相似?如果一定相似,请予以证明;如果不一定相似或一定不相似,请简要说明理由;
 (4)当点P在曲线上移动时,△OEF随之变动,指出在△OEF的三个内角中,大小始终保持不变的那个角和它的大小,并证明你的结论。(12分)
(4)当点P在曲线上移动时,△OEF随之变动,指出在△OEF的三个内角中,大小始终保持不变的那个角和它的大小,并证明你的结论。(12分)
29、(本题12分)同学们都做过人教版《几何》第三册102页第2题:“如图,OA、OB是⊙O的半径,并且OA⊥OB,P是OA上任一点,BP的延长线交⊙O于Q,过Q的⊙O的切线交OA的延长线于R,求证:RP=RQ”。
试问:在其他条件不变的情况下
(1) 将直线RP向上平移,一端在半径OB上(如图1), RP与RQ之间存在什么关系?
(2) 再将直线RP平移至⊙O外(如图2),这时RP与RQ之间存在什么关系?
请分别证明你的结论。

28、(本题10分)老李在商场内购买一种商品,与营业员有下面一段对话:
老 李:上个月还挺贵,这次便宜多了,一次降价幅度就达到19%。
营业员:不,这中间又降了一次价,两次降价幅度相同。
老 李:数量大的话,还有优惠吗?
营业员:目前有两种优惠办法:①如果不要送货上门的话,价格可以再优惠5%,但为了运输安全和方便,需要预付90元的专用包装材料费;②如果要送货上门,价格只能再优惠2%,但可以免费使用专用包装。
(1)根据这段对话,求这种商品每次降价的百分率。
(2)设优惠前老李的购物金额为 元,优惠后不送货上门需支付
元,优惠后不送货上门需支付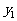 元;送货上门需支付
元;送货上门需支付 元,用代数式分别表示
元,用代数式分别表示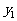 、
、 与
与 之间的关系。
之间的关系。
(3)根据优惠前老李的购物金额,享受哪种优惠更实惠。(运输费不考虑)
27、(本题10分)如图,已知:AO为⊙O1的直径,⊙O1与⊙O的一个交点为E,直线AO交⊙O于B、C两点,⊙O的切线GF交直线AO于点D,与AE的延长线垂直相交于点F.
(1)求证:AE是⊙O的切线;
(2)若AB=2,AE=6,求△ODG的周长.

26、 (本题8分)如图,在⊿ABC中,∠A的平分线AM与BC交于点M,且与⊿ABC的外接圆O交于点D。过D作⊙O的切线交AC的延长线于E,连结DC,求证:
(本题8分)如图,在⊿ABC中,∠A的平分线AM与BC交于点M,且与⊿ABC的外接圆O交于点D。过D作⊙O的切线交AC的延长线于E,连结DC,求证:
要求:请根据题目所给的条件和图形,在题中的横线上写出一个正确的结论,并加以证明(在写结论和证明时都不能在图中添加其它字母和线段),按证明结论时需要用到的已知条件的多少给分,若用足已知条件而证得结论即可得满分。

25、(本题8分)已知方程:mx2+2(m-1)x+m-3=0。
(1)m取什么值时,方程有两个实数根?
(2)m取什么值时,方程的两个实数根的平方和等于4?
24、(本题8分)
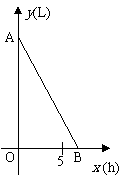
(1)甲品牌拖拉机开始工作时,油箱中有油30升。如果每小时耗油6升,求油箱中的余油量y(升)与工作时间x(时)之间的函数关系式。
(2)如图,线段AB表示乙品牌拖拉机在工作时油箱中的余油量y(升)与工作时间x(时)之间的函数关系的图象。若甲、乙两种品牌的拖拉机在售价、质量、性能、售后服务等条件上都一样。根据图象提供的信息,你愿意购买哪种品牌的拖拉机,并说明理由。
23、(本题8分)为缓解“停车难”问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图。按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入。(其中AB=9m,BC=0.5m)为标明限高,请你根据该图计算CE.(精确到0.1m, sin18º=0.3090, cos18º=0.9510, tan18º=0.3249, cot18º=3.078)

22、(本题7分)解方程
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com