
题目列表(包括答案和解析)
4.一个口袋中有6个白球,6个黑球,下列事件中的必然事件是…………………[ ]
A.从口袋中摸出6个球,其中3个白球,3个黑球
B.从口袋中摸出6个球,全部都是黑球
C.从口袋中摸出6个球,全部都是白球
D.从口袋中摸出7个球,至少有一个是白球
3.第五次全国人口普查结果显示,我国的总人口已达到13亿人,用科学计数法表示这个数,正确的是…………………………………………………………………………………[ ]
A.1.3×108 B.1.3×109 C.0.13×1010 D.13×108
2.下列运算正确的是……………………………………………………………………[ ]
A.(-x2)3=-x6 B.x8÷x4=x2 C.x3+x3=2x6 D.(xy)3=xy3
1.计算(-2)3的值是………………………………………………………………………[ ]
A.-6 B.6 C.-8 D.8
27.(本题满分12分)
如图,△OAB是边长为 的等边三角形,其中O是坐标原点,顶点B在Y轴的正半轴上,将△OAB折叠,使点A落在边OB上,记为D,折痕为EF。
的等边三角形,其中O是坐标原点,顶点B在Y轴的正半轴上,将△OAB折叠,使点A落在边OB上,记为D,折痕为EF。
(1)当DE∥X轴时,求点D和E的坐标
(2)当DE∥X轴时,求线段DF的长及直线DF的解析式;
 (3)当D在OB上运动但不与O、B重合时,能不能使△DEF成为直角三角形?若能,请求出此时点D的坐标:若不能,请你说明理由。
(3)当D在OB上运动但不与O、B重合时,能不能使△DEF成为直角三角形?若能,请求出此时点D的坐标:若不能,请你说明理由。
26.(本题满分12分)
已知,如图⊙O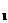 与⊙O
与⊙O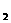 外切于点A,BC是⊙O
外切于点A,BC是⊙O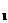 和⊙O
和⊙O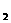 的公切线,B、C为切点。
的公切线,B、C为切点。
(1)求证:AB⊥AC;
(2)若 、
、 分别为⊙O
分别为⊙O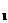 、⊙O
、⊙O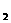 的半径,且
的半径,且 =2
=2 ,求
,求 的值。
的值。

25.(本题满分10分)
已知抛物线
(1)求证:该抛物线与x轴一定有两个交点;
(2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积。
23.(本题满分8分)
 已知△ABC中,∠A的平分线AD交BC于D,⊙O过点A,且和BC切于D,和AB、AC分别交于E、F.
已知△ABC中,∠A的平分线AD交BC于D,⊙O过点A,且和BC切于D,和AB、AC分别交于E、F.
求证:EF∥BC
24*.(人教版:本题满分10分)
甲、乙两人分别从相距27千米的A、B两地同时出发相向而行,3小时后相遇,相遇后两人按原来的速度继续前进,甲到达B地比乙到达A地早1小时21分,求两人的速度。
(1)设甲的速度是x千米/小时,乙的速度是y千米/小时,根据题意,利用速度、时间、路程之间的关系填写下表(要求用适当的代数式,完成表格):
|
|
速度(千米/时) |
所用时间(时) |
所走的路程(千米) |
|
|
相遇时 |
甲 |
x |
3 |
|
|
乙 |
y |
3 |
|
|
|
走完全程时 |
甲 |
x |
|
27 |
|
乙 |
y |
|
27 |
(2)列出方程(组),并求出问题的解。
24*.(华师版:本题满分10分)
 现有足够的2×2,3×3的正方形和2×3的矩形图片A、B、C,如图所示,从中各选取若干个图片拼成不同的图形。请你在下面给出的方格纸中,按下面的要求分别画出一种示意图(说明:下面给出的方格纸中,每个正方形的边长为1。拼出的图形,要求每两片之间无缝隙,也不重叠。画图必须保留拼图的痕迹):
现有足够的2×2,3×3的正方形和2×3的矩形图片A、B、C,如图所示,从中各选取若干个图片拼成不同的图形。请你在下面给出的方格纸中,按下面的要求分别画出一种示意图(说明:下面给出的方格纸中,每个正方形的边长为1。拼出的图形,要求每两片之间无缝隙,也不重叠。画图必须保留拼图的痕迹):
(1)选取A、B型各1片,C型2片,在图1中拼成一个正方形。
(2)选取A型4片,B型1片,C型4片,在图2中拼成一个正方形。
(3)选取A型3片,B型1片,C型若干,在图3中拼成一个矩形。

21.(本题满分6分)
解方程: 
22*.(人教版:本题满分8分)
夏雪同学调查了班级同学身上有多少零用钱,将每位同学的零用钱记录下来,下面是全班40名同学的零用钱的数目(单位:元)
2,5,0,5,2,5,6,5,0,5,5,52,5,8,0,5,5,2,5,
5,8,6,5,2,5,5,2,5,6,5,5,0,6,5,6,5,2,5,0.
(1)请你写出同学的零用钱(0元,2元,5元,6元8元)出现的频数;
(2)求出同学的零用钱的平均数、中位数和众数;
(3)假如老师随机问一个同学的零用钱,老师最有可能得到的回答是多少元?
22*.(华师版:本题满分8分)
某校每学期都要对优秀的学生进行表扬,每班采取民主投票的方式进行选举,若每个班级平均分到3位三好生、4位模范生、5位成绩提高奖的名额,且各项均不能兼得,现在学校有30个班级,平均每班50人。
(1)作为一名学生,你恰好能得到荣誉的机会有多大?
(2)作为一名学生,你恰好能当选三好生或模范生的机会各有多大?
(3)在全校学生数、班级人数、三好生数、模范生数、成绩提高奖人数中,哪些是解决上面两个问题所需要的?
(4)你可以用哪些方法来模拟实验?(举出一例加以说明)
20.(本题满分6分)
如图,正方形ABCD中,BE=BF,BG⊥EC,
求证:BF︰DC=EG︰BG.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com